Simplexní metoda - pravidlo pro výběr rozlišovacího řetězce. Gauss-Jordanova metoda. Příklady řešení soustav lineárních algebraických rovnic metodou Gauss-Jordan. Simplexová metoda, řešení problému s umělým základem

Chcete-li začít, musíte tento systém omezení byla vyjádřena rovností a v tomto systému omezení by měly být identifikovány základní neznámé. Řešení úlohy simplexovou metodou je rozděleno do několika kroků. Při každém kroku se z této báze B přesouvají do jiné, nové báze B 1 s takovým výpočtem, že hodnota funkce Z klesá, tzn. . Pro přechod na nový základ je jedna z proměnných odstraněna ze staré báze a místo ní je zavedena jiná z volných. Po konečném počtu kroků je nalezena určitá báze B (k), pro kterou existuje požadované minimum pro lineární funkci Z, a odpovídající základní řešení je optimální nebo se ukáže, že problém nemá řešení.

4.1 Algoritmus simplexové metody.

Dovolte mi zvážit systém omezení a lineární formu formuláře:

(4.1)

Jordan-Gaussovou metodou redukujeme psaný systém do podoby, kdy jsou zvýrazněny základní proměnné.

Pojďme si představit některé konvence:

–základní proměnné;

– volné proměnné.

(4.4)

Pomocí posledního systému omezení sestrojíme tabulku. 4.1.

Tabulka 4.1

Simplexní stůl

Dostupný Základní neznámý	Volný, uvolnit

Tato tabulka se nazývá simplexní tabulka. Všechny další transformace jsou spojeny se změnami v obsahu této tabulky.

Algoritmus simplexové metody je následující.

1. Poslední řádek simplexní tabulky obsahuje nejmenší kladný prvek, nepočítaje volný termín. Sloupec odpovídající tomuto prvku je považován za přípustný.

2. Vypočítejte poměr volných členů ke kladným prvkům rozlišovacího sloupce (simplexní poměr). Najděte nejmenší z těchto simplexních vztahů, který odpovídá řetězci rozlišení;

3. Na průsečíku rozlišovacího řádku a sloupce je rozlišovací prvek.

4. Pokud existuje několik simplexních relací stejné velikosti, vyberte kteroukoli z nich a poté vyberte kteroukoli z nich. Totéž platí pro kladné prvky posledního řádku simplexní tabulky.

5. Po nalezení rozlišovacího prvku přejděte k další tabulce. Neznámé proměnné odpovídající aktivovanému odlivu a sloupci jsou zaměněny. V tomto případě se základní proměnná stává volnou proměnnou a naopak. Simplexová tabulka je převedena následovně

Tabulka 4.2

Simplexní stůl

Dostupný Základní neznámý	Volný, uvolnit

6. Prvek tabulky 4.2 odpovídající povolujícímu prvku tabulky. 4.1, se rovná vzájemné hodnotě rozlišovacího prvku.

7. Prvky řádku tabulky. 4.2, odpovídající prvkům tabulky povolovacích toků. 4.1 získáme dělením odpovídajících prvků tabulky. 4.1 k rozlišovacímu prvku.

8. Prvky sloupců tabulky. 4.2, odpovídající prvkům sloupce rozlišení v tabulce. 4.1 získáme dělením odpovídajících prvků tabulky. 4.1 k rozlišovacímu prvku a jsou brány s opačným znaménkem.

9. Zbývající prvky se vypočítají podle pravidla obdélníku: mentálně nakreslíme obdélník v tabulce 4.2, jehož jeden vrchol se shoduje s rozlišovacím prvkem a druhý s prvkem, jehož obrázek hledáme; zbývající dva vrcholy jsou jednoznačně určeny. Poté požadovaný prvek tabulky. 4.2 se bude rovnat odpovídajícímu prvku tabulky. 4.1 mínus zlomek ve jmenovateli, který obsahuje rozlišovací prvek, a v čitateli součin prvků ze dvou nepoužitých vrcholů obdélníku.

10. Jakmile je získána tabulka, ve které jsou všechny prvky v posledním řádku záporné, má se za to, že bylo nalezeno minimum. Minimální hodnota funkce je rovna fiktivnímu termínu v řetězci Objektivní funkce, a optimální řešení je určeno volnými členy základních proměnných. Všechny volné proměnné jsou v tomto případě rovny nule.

11. Pokud jsou všechny prvky ve sloupci rozlišení záporné, pak problém nemá řešení (není dosaženo minima).

5. Metody hledání referenční roztok problémy lineárního programování.

5.1. Metoda umělé báze.

Algoritmus Simplexové metody formulovaný výše lze použít pouze tehdy, je-li první platné řešení, tj. původní problém lineární programování připomněl

Zároveň tedy, položíme-li volné neznámé na nulu, získáme referenční řešení.

Budu zvažovat metodu pro nalezení referenčního řešení založenou na zavedení umělých proměnných. Za tímto účelem zapíšeme problém lineárního programování obecný pohled. Budeme zvažovat problém s řadou neznámých a omezení:

(5.1)

Přepišme systém (5.1) do jiné podoby. Za tímto účelem zavádíme umělé proměnné, aby byl identifikován základ. Poté systém převezme formu

(5.2)

Systémy (5.1) a (5.2) budou ekvivalentní, pokud se všechna pro rovnají 0. Navíc se domnívám, že všechna pro. Jinak odpovídající omezení ze systému (5.1) vynásobíme – 1. Aby se rovnaly 0, musíme problém transformovat tak, aby se všechny umělé proměnné staly volnými neznámými.

V tomto případě bude mít systém (5.2) po transformaci tvar:

(5.3)

Vždy můžete přejít ze systému (5.2) do systému (5.3) pomocí kroků simplexní metody. S takovým přechodem jako lineární tvar zvážit funkci

rovnající se součtu umělých proměnných. Přechod je dokončen, když jsou všechny umělé proměnné převedeny na volné neznámé.

Analýza možností řešení

1. Pokud jsou , a všechny převedeny na volné proměnné, pak problém nemá kladné řešení.

2. Pokud , a část zůstane v základu, pak k jejich převedení na volné je nutné použít speciální techniky.

V simplexní tabulce odpovídající systému (5.3) za , a všechny jsou volné, škrtněte řádek pro a sloupce pro a vyřešte úlohu pro původní lineární tvar.

5.2. Druhý vyhledávací algoritmus referenční plán.

Nechť je problém lineárního programování napsán v kanonické podobě:

(5.5)

Sestavme první Jordan-Gaussovu tabulku pro úlohy (5.5) a (5.6). Abychom zajistili jednotnost výpočetního postupu, přiřadíme zdrojové tabulce řádek cílové funkce:

Po převedení systému omezení na jednotkovou bázi bude účelová funkce, stejně jako základní proměnné, vyjádřena pomocí volných proměnných. Podobnou techniku ​​jsem použil při řešení úloh pomocí grafické metody s více než dvěma proměnnými.

Algoritmus metody

1. Zapišme úlohu ve tvaru (5.7) a všechny prvky sloupce volných členů musí být nezáporné. Rovnice soustavy (5.5), ve které jsou volné členy záporné, je třeba nejprve vynásobit – 1.

2. Transformujeme tabulku (5.7) pomocí Jordan-Gaussových eliminačních kroků. V tomto případě lze v každém kroku vybrat jako rozlišující libovolný sloupec obsahující alespoň jeden kladný prvek. Řádek cílové funkce neovlivňuje výběr sloupců rozlišení.

3. Rozlišovací řádek je určen nejmenším z poměrů volných členů k prvkům rozlišovacího sloupce.

4. Při procesu transformace škrtáme řádky skládající se pouze z nul.

5. Pokud v procesu transformací narazíte na řetězec, ve kterém jsou všechny prvky nulové a volný člen je nenulový, pak problém nemá řešení. Pokud narazíte na řádek, ve kterém jsou kromě volného člena další pozitivní prvky ne, pak říkají, že problém nemá žádná pozitivní řešení.

Vysvětlení. V odstavci 1.1 algoritmu se předpokládá, že všechny prvky sloupce volných členů jsou nezáporné. Tento požadavek je volitelný. V případě, že jsou ve sloupci volných členů záporná čísla, použijeme větu.

Teorém. Pokud je rozlišovací prvek vybrán podle nejmenšího kladného simplexního poměru, pak se po Jordan-Gaussově kroku volný člen v rozlišovací linii stane kladným a zbývající členy si ponechají své znaménko.

Volba rozlišovacího prvku se provádí odlišně, a to.

1. Podívejte se na řádek odpovídající libovolnému zápornému volnému termínu. Vyberte v něm libovolný záporný prvek - bude se řešit sloupec odpovídající tomuto prvku.

2. Volba rozlišovacího prvku se provádí podle minimálního kladného simplexního poměru. Pokud je problém řešitelný, pak po konečném počtu kroků je získáno první proveditelné řešení a lze použít simplexovou metodu.

V některých případech je prvním takto nalezeným proveditelným řešením také optimální řešení.

Na grafická metoda pro řešení LP úloh jsme vlastně vybrali z množiny vrcholů patřících k hranici množiny řešení soustavy nerovnic vrchol, ve kterém hodnota účelové funkce dosáhla maxima (minima). V případě dvou proměnných je tato metoda zcela intuitivní a umožňuje rychle najít řešení problému.

Pokud jsou v problému tři nebo více proměnných, a ve skutečnosti ekonomické úkoly Právě v takové situaci je obtížné vizualizovat oblast řešení systému omezení. Takové problémy se řeší pomocí simplexní metoda nebo metodou postupného vylepšování. Myšlenka metody je jednoduchá a je následující.

Podle určitého pravidla je nalezen výchozí referenční plán (nějaký vrchol omezující oblasti). Kontroluje, zda je plán optimální. Pokud ano, problém je vyřešen. Pokud ne, tak přejdeme k dalšímu vylepšenému plánu – k dalšímu vrcholu. hodnota účelové funkce na této rovině (v tomto vrcholu) je samozřejmě lepší než v předchozí. Algoritmus přechodu se provádí pomocí určitého výpočetního kroku, který je pohodlně zapsán ve formě tabulek tzv. simplexní stoly . Protože existuje konečný počet vrcholů, v konečném počtu kroků dojdeme k optimálnímu řešení.

Uvažujme simplexní metoda na konkrétní příkladúkoly týkající se sestavení plánu.

Ještě jednou poznamenejme, že k řešení lze použít simplexovou metodu kanonické problémy LP redukované do speciální formy, tj. mající základ, kladné pravé strany a objektivní funkci vyjádřenou v termínech nezákladních proměnných. Pokud není úkol zredukován na speciální formulář, jsou potřeba další kroky, o kterých si povíme později.

Podívejme se na problém výrobního plánu, když jsme předtím zkonstruovali model a dovedli jej do speciální podoby.

Úkol.

Pro výrobu produktů A A V Sklad může uvolnit více než 80 jednotek surovin. Navíc na výrobu produktu A spotřebovávají se dvě jednotky a produkty V- jedna jednotka surovin. Výrobu je nutné plánovat tak, aby byl zajištěn co největší zisk produktů A je nutné vyrobit maximálně 50 kusů a výrobků V- ne více než 40 ks. Navíc zisk z prodeje jednoho produktu A- 5 rublů a od V- 3 rub.

Pojďme stavět matematický model, označující jako X 1 množství výrobků A v plánu, pro X 2 - počet výrobků V. pak bude omezovací systém vypadat takto:

Snižme problém na kanonická forma zavedením dalších proměnných:

(3.10)

F = -5x 1 - 3x 2 → min.

Tento problém má zvláštní formu (se základem, pravé strany jsou nezáporné). Lze to řešit simplexovou metodou.

jáetapa. Záznam problému do simplexní tabulky. Mezi systémem omezení problému (3.10) a simplexní tabulkou existuje vzájemná shoda. V tabulce je tolik řádků, kolik je rovností v systému omezení, a sloupců je tolik, kolik je volných proměnných. Základní proměnné vyplňují první sloupec, volné - horní linie tabulky. Spodní řádek se nazývá indexový řádek; zapisují se do něj koeficienty proměnných v účelové funkci. V pravém dolním rohu se zpočátku zapisuje 0, pokud ve funkci není žádný volný člen; pokud existuje, napište jej s opačným znaménkem. Na tomto místě (v pravém dolním rohu) bude hodnota účelové funkce, která by měla při přechodu z jedné tabulky do druhé narůst v absolutní hodnotě. Tabulka 3.4 tedy odpovídá našemu systému omezení a můžeme přejít do fáze II řešení.

Tabulka 3.4

základní			volný, uvolnit

IIetapa. Kontrola optimálnosti referenčního plánu.

Tato tabulka 3.4 odpovídá následujícímu referenčnímu plánu:

(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).

Volné proměnné X 1 , X 2 se rovná 0; X 1 = 0, X 2 = 0. A základní proměnné X 3 , X 4 , X 5 nabývat hodnot X 3 = 50, X 4 = 40, X 5 = 80 - ze sloupce volné termíny. Hodnota objektivní funkce:

-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.

Naším úkolem je ověřit, zda je daný referenční plán optimální. Chcete-li to provést, musíte se podívat na řádek indexu - řádek cílové funkce F.

Jsou možné různé situace.

1. V rejstříku F- v řetězci nejsou žádné negativní prvky. To znamená, že plán je optimální a řešení problému lze sepsat. Cílová funkce dosáhla svého cíle optimální hodnotu, rovné číslu v pravém dolním rohu, brané s opačným znaménkem. Přejděme do fáze IV.

2. Řádek indexu má alespoň jeden záporný prvek, jehož sloupec neobsahuje žádné kladné prvky. Pak dojdeme k závěru, že účelová funkce F→∞ klesá bez omezení.

3. Řádek indexu obsahuje záporný prvek, který má ve svém sloupci alespoň jeden kladný prvek. Poté přejdeme do další fáze III. Přepočítáváme tabulku a vylepšujeme referenční plán.

IIIetapa. Zlepšení referenčního plánu.

Z negativních prvků indexu F-řádky, vyberte ten s největším modulem, zavolejte odpovídající rozlišení sloupců a označte jej „“.

Pro výběr rozlišovacího řádku je nutné vypočítat poměry prvků sloupce volných výrazů pouze Na pozitivní prvky sloupce rozlišení. Ze získaných vztahů vyberte tu minimální. Odpovídající prvek, při kterém je dosaženo minima, se nazývá rozlišení. Zvýrazníme jej čtverečkem.

V našem příkladu , prvek 2 je povolený. Čára odpovídající tomuto prvku se také nazývá rozlišení (tab. 3.5).

Tabulka 3.5

Po výběru povolovacího prvku přepočítáme tabulku podle pravidel:

1. V nové tabulce stejné velikosti jako doposud se prohodí proměnné rozlišovacího řádku a sloupce, což odpovídá přechodu na nový základ. V našem příkladu: X 1 je zahrnuta do základu X 5, který opouští základ a je nyní zdarma (tabulka 3.6).

Tabulka 3.6

základní			volný, uvolnit

2. Místo rozlišovacího prvku 2 napište jeho převrácené číslo.

3. Prvky rozlišovací čáry dělíme rozlišovacím prvkem.

4. Prvky sloupce rozlišení rozdělíme prvkem rozlišení a zapíšeme je opačným znaménkem.

5. Pro vyplnění zbývajících prvků tabulky 3.6 provedeme přepočet pomocí pravidla obdélníku. Řekněme, že chceme počítat prvek na pozici 50.

Tento prvek mentálně spojíme s rozlišovacím, najdeme součin, odečteme součin prvků umístěných na druhé diagonále výsledného obdélníku. Rozdíl dělíme rozlišovacím prvkem.

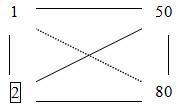
Tak, . Napíšeme 10 na místo, kde jich bylo 50. Podobně :

, , , .

Tabulka 3.7

My máme nový stůl 3.7, základními proměnnými jsou nyní proměnné (x 3,x 4,x 1). Hodnota účelové funkce se stala rovnou -200, tj. klesla. Abychom zkontrolovali optimalitu tohoto základního řešení, musíme znovu přejít do fáze II. Proces je zjevně konečný;

Dokončeme řešení problému. Chcete-li to provést, zkontrolujte řádek indexu a když v něm vidíme záporný prvek, zavolejte odpovídající rozlišení sloupce a podle Stupeň III, přepočítáme tabulku. Po sestavení vztahů a zvolení minima = 40 z nich jsme určili rozlišovací prvek 1. Nyní provedeme přepočet podle pravidel 2-5.

Tabulka 3.8

základní			volný, uvolnit
	x 3 = 30, X 2 = 40, X 1 = 20. Volné proměnné jsou 0, X 5 = 0, X 4 = 0. Cílová funkce nabývá hodnoty poslední prvek sloupec volných výrazů s opačným znaménkem: - F = -220 F = 220, v našem příkladu byla funkce zkoumána při min a zpočátku F max, takže znak se ve skutečnosti změnil dvakrát. Tak, X* = (20, 40, 30, 0, 0), F* = 220. Odpověď na problém: Do výrobního plánu je nutné zařadit 20 výrobků daného druhu A, 40 produktů typu B, přičemž zisk bude maximální a bude se rovnat 220 rublům. Na konci této části uvádíme vývojový diagram algoritmu simplexní metody, který přesně opakuje kroky, ale možná pro některé čtenáře bude pohodlnější, protože šipky ukazují jasný směr akcí. Odkazy nad rámečky ve vývojovém diagramu označují, do které fáze nebo dílčího bodu příslušná skupina transformací patří. pravidlo pro nalezení výchozího referenčního plánu bude formulováno v odstavci 3.7. Otázky pro sebeovládání 1. Jak se konstruuje simplexní tabulka? 2. Jak se změna základu projeví v tabulce? 3. Formulujte zastavovací kritérium pro simplexovou metodu. 4. Jak uspořádat přepočet tabulky? 5. Od kterého řádku je vhodné začít přepočítávat tabulku?

V obecný případ lineární rovnice je:

Rovnice má řešení: pokud je alespoň jeden z koeficientů neznámých odlišný od nuly. V tomto případě se jakýkoli -rozměrný vektor nazývá řešením rovnice, pokud se při dosazení jeho souřadnic rovnice stane identitou.

Obecná charakteristika řešené soustavy rovnic

Příklad 20.1

Popište soustavu rovnic.

Řešení:

1. Je v tom nějaká protichůdná rovnice?(Pokud koeficienty, v tomto případě má rovnice tvar: a nazývá se kontroverzní.)

• Pokud systém obsahuje něco protichůdného, ​​pak je takový systém nekonzistentní a nemá řešení.

2. Najděte všechny povolené proměnné. (Neznámý se nazývápovoleno pro soustavu rovnic, pokud je zahrnuta v jedné z rovnic soustavy s koeficientem +1, ale není zahrnuta ve zbývajících rovnicích (tj. je zahrnuta s koeficientem rovným nule).

3. Je soustava rovnic vyřešena? (Soustava rovnic se nazývá vyřešená, pokud každá rovnice soustavy obsahuje vyřešenou neznámou, mezi kterými nejsou žádné shodné)

Vytvoří se vyřešené neznámé, z každé rovnice systému jedna plný set vyřešené neznámé systémy. (v našem příkladu je to toto)

Povolené neznámé zahrnuté v kompletní sadě jsou také nazývány základní() a není součástí sady - volný, uvolnit ().

V obecném případě má vyřešená soustava rovnic tvar:

Na v tomto stádiu hlavní věcí je pochopit, co to je vyřešeno neznámo(zahrnuto v základu a zdarma).

Obecné Konkrétní Základní řešení

Obecné řešení vyřešená soustava rovnic je množina vyjádření vyřešených neznámých prostřednictvím volných členů a volných neznámých:

Soukromé rozhodnutí se nazývá řešení, které se získá z obecného řešení pro konkrétní hodnoty volných proměnných a neznámých.

Základní řešení se nazývá konkrétní řešení získané z obecného s nulové hodnoty volné proměnné.

• Základní řešení (vektor) se nazývá degenerovat, pokud je počet jeho nenulových souřadnic menší než počet povolených neznámých.
• Základní řešení je tzv nedegenerované, pokud je počet jeho nenulových souřadnic roven počtu povolených neznámé systémy součástí kompletní sady.

Věta (1)

Vyřešený systém rovnic je vždy konzistentní(protože má alespoň jedno řešení); Navíc, pokud systém nemá volné neznámé,(to znamená, že v systému rovnic jsou v základu zahrnuty všechny povolené) pak je to definováno(má unikátní řešení); pokud existuje alespoň jedna volná proměnná, pak systém není definován(má nekonečně mnoho řešení).

Příklad 1. Najděte obecné, základní a libovolné konkrétní řešení soustavy rovnic:

Řešení:

1. Kontrolujeme, zda je systém autorizován?

• Systém je vyřešen (protože každá z rovnic obsahuje vyřešenou neznámou)

2. Do množiny zařazujeme povolené neznámé – z každé rovnice jednu.

3. Obecné řešení zapisujeme podle toho, jaké povolené neznámé jsme do množiny zařadili.

4. Hledání soukromého řešení. Abychom to udělali, zrovnoprávníme volné proměnné, které jsme do množiny nezahrnuli, s libovolnými čísly.

Odpovědět: soukromé řešení(jedna z možností)

5. Nalezení základního řešení. Za tímto účelem srovnáme volné proměnné, které jsme do množiny nezahrnuli, s nulou.

Elementární transformace lineárních rovnic

Systémy lineárních rovnic jsou redukovány na ekvivalentní řešené systémy pomocí elementární transformace.

Věta (2)

Jestli nějaký vynásobte rovnici soustavy nějakým nenulovým číslem, a zbytek rovnic ponechte beze změny, pak . (tedy pokud vynásobíte levou a pravá strana rovnice pro stejné číslo, pak dostanete rovnici ekvivalentní danému)

Věta (3)

Li přidat další do libovolné rovnice soustavy a všechny ostatní rovnice ponechte beze změny dostaneme systém ekvivalentní tomuto. (to znamená, že pokud přidáte dvě rovnice (přičtením jejich levé a pravé strany), dostanete rovnici ekvivalentní datům)

Důsledek vět (2 a 3)

Li přidat další rovnici k rovnici vynásobené určitým číslem a všechny ostatní rovnice ponechte beze změny, pak dostaneme systém ekvivalentní tomuto.

Vzorce pro přepočet systémových koeficientů

Pokud máme soustavu rovnic a chceme ji převést na vyřešenou soustavu rovnic, pomůže nám s tím Jordan-Gaussova metoda.

Jordanova transformace s rozlišovacím prvkem umožňuje získat vyřešenou neznámou pro soustavu rovnic v rovnici s číslem . (příklad 2).

Jordanova transformace se skládá z elementárních transformací dvou typů:

Řekněme, že chceme z neznámé v nižší rovnici udělat vyřešenou neznámou. Abychom to udělali, musíme vydělit , takže součet je .

Příklad 2 Přepočítejme systémové koeficienty

Při dělení rovnice číslem číslem se její koeficienty přepočítají pomocí vzorců:

Chcete-li vyloučit z rovnice s číslem , musíte rovnici s číslem vynásobit a přidat k této rovnici.

Věta (4) O snížení počtu rovnic soustavy.

Pokud soustava rovnic obsahuje triviální rovnici, lze ji ze soustavy vyloučit a získáme soustavu ekvivalentní té původní.

Věta (5) O nekompatibilitě soustavy rovnic.

Pokud soustava rovnic obsahuje nekonzistentní rovnici, pak je nekonzistentní.

Algoritmus Jordan-Gaussovy metody

Algoritmus pro řešení soustav rovnic pomocí Jordan-Gaussovy metody se skládá z řady podobných kroků, z nichž každý se provádí v následujícím pořadí:

1. Zkontroluje, zda systém není konzistentní. Pokud systém obsahuje nekonzistentní rovnici, pak je nekonzistentní.
2. Kontroluje se možnost snížení počtu rovnic. Pokud soustava obsahuje triviální rovnici, je přeškrtnuta.
3. Je-li soustava rovnic vyřešena, zapište obecné řešení soustavy a případně řešení partikulární.
4. Pokud systém není vyřešen, pak v rovnici, která neobsahuje vyřešenou neznámou, se vybere rozlišovací prvek a s tímto prvkem se provede Jordanova transformace.
5. Poté se vraťte k bodu 1

Příklad 3 Řešte soustavu rovnic Jordan-Gaussovou metodou.

Nalézt: dvě obecná a dvě odpovídající základní řešení

Řešení:

Výpočty jsou uvedeny v tabulce níže:

Napravo od tabulky jsou akce s rovnicemi. Šipky ukazují, ke které rovnici je rovnice s rozlišovacím prvkem přidána, vynásobená vhodným faktorem.

První tři řádky tabulky obsahují koeficienty pro neznámé a pravou stranu původní systém. Výsledky první Jordanovy transformace s rozlišovacím prvkem rovný jedné jsou uvedeny na řádcích 4, 5, 6. Výsledky druhé Jordanovy transformace s rozlišovacím prvkem rovným (-1) jsou uvedeny na řádcích 7, 8, 9. Jelikož je třetí rovnice triviální, lze ji ignorovat.

Gauss-Jordanova metoda je navržena pro řešení lineárních systémů algebraické rovnice(SLAU). Jde o modifikaci Gaussovy metody. Pokud se Gaussova metoda provádí ve dvou fázích (dopředu a dozadu), pak vám metoda Gauss-Jordan umožňuje vyřešit systém v jedné fázi. Podrobnosti a přímá aplikace Gauss-Jordanovy metody jsou popsány v příkladech.

Ve všech příkladech $A$ označuje systémovou matici, $\widetilde(A)$ rozšířenou systémovou matici. O matricové formě záznamu SLAE si můžete přečíst.

Příklad č. 1

Vyřešte SLAE $ \left\( \začátek(zarovnáno) & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end(zarovnáno ) \right.$ metodou Gauss-Jordan.

Přejděme od poslední matice, kterou jsme obdrželi, k systému:

$$ \left\( \begin(zarovnáno) & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2; \\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1 \end(zarovnáno) \vpravo $$.

Pro zjednodušení výsledného systému máme:

$$ \left\( \začátek(zarovnáno) & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end(zarovnáno) \vpravo. $$

Kompletní řešení bez vysvětlení to vypadá takto:

Ačkoli je tento způsob výběru rozlišovacích prvků zcela přijatelný, je vhodnější vybrat jako rozlišovací prvky diagonální prvky systémové matice. Na tuto metodu se podíváme níže.

Výběr rozlišovacích prvků na hlavní diagonále matice systému.

Jelikož je tento způsob řešení zcela podobný předchozímu (kromě volby rozlišovacích prvků), tak podrobná vysvětlení přeskočme to. Princip výběru povolovacích prvků je jednoduchý: v prvním sloupci vybereme prvek prvního řádku, ve druhém sloupci vezmeme prvek druhého řádku, ve třetím sloupci prvek třetího řádku atd. na.

První krok

V prvním sloupci vyberte prvek prvního řádku, tzn. máme prvek 4 jako rozlišovací prvek Chápu, že volba čísla 2 se zdá výhodnější, protože toto číslo je stále menší než 4. Aby se číslo 2 v prvním sloupci posunulo na první místo, prohodíme první. a druhé řady:

$$ \left(\begin(pole) (ccc|c) 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end(pole) \ vpravo)\šipka vpravo \left(\začátek(pole) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end(pole ) \vpravo)$$

Aktivační prvek je tedy reprezentován číslem 2. Stejným způsobem jako dříve vydělte první řádek 2 a potom vynulujte prvky prvního sloupce:

$$ \left(\begin(pole) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end(pole) \ vpravo) \begin(pole) (l) I:2 \\\phantom(0) \\ \phantom(0) \end(pole) \rightarrow \left(\begin(pole) (ccc|c) 1 & - 2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end(pole) \vpravo) \begin(pole) (l) \phantom(0 ) \\ II-4\cdot I\\ III+3\cdot I \end(pole) \rightarrow \left(\begin(pole) (ccc|c) 1 & -2& 5/2 & -13/2\ \0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end(pole) \vpravo). $$

Druhý krok

Druhý krok vyžaduje vynulování prvků druhého sloupce. Jako rozlišovací prvek vybereme prvek druhého řádku, tzn. 1. Aktivační prvek již je rovný jedné, takže nebudeme vyměňovat žádné řádky. Mimochodem, pokud bychom chtěli prohodit řádky, nedotkli bychom se prvního řádku, protože už byl použit v prvním kroku. Ale druhý a třetí řádek lze snadno prohodit. Opakuji však, že v této situaci není potřeba přehazovat řádky, protože rozlišovací prvek je již optimální - rovná se jedné.

$$ \left(\begin(pole) (ccc|c) 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/ 2 \end(pole) \right) \begin(array) (l) I+2\cdot II \\ \phantom(0)\\ III-5\cdot II \end(pole) \rightarrow \left(\begin (pole) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end(pole) \že jo). $$

Druhý krok je dokončen. Přejděme ke třetímu kroku.

Třetí krok

Třetí krok vyžaduje vynulování prvků třetího sloupce. Jako rozlišovací prvek vybereme prvek třetího řádku, tzn. 37/2. Vydělte prvky třetího řádku 37/2 (tak, aby se rozlišovací prvek rovnal 1) a poté vynulujte odpovídající prvky třetího sloupce:

$$ \left(\begin(pole) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37 /2 \end(pole) \right) \begin(pole) (l) \phantom(0)\\ \phantom(0)\\ III:\frac(37)(2) \end(pole) \rightarrow \ left(\begin(pole) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end(pole) \right) \begin(pole) (l) I+2\cdot III\\II+3/2\cdot III\\ \phantom(0) \end(pole) \rightarrow \left(\begin(pole) ( ccc|c) 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end(pole) \vpravo). $$

Obdržená odpověď: $x_1=-2$, $x_2=1$, $x_3=-1$. Kompletní řešení bez vysvětlení vypadá takto:

Všechny ostatní příklady na této stránce budeme řešit přesně druhým způsobem: jako rozlišovací vybereme diagonální prvky systémové matice.

Odpovědět: $x_1=-2$, $x_2=1$, $x_3=-1$.

Příklad č. 2

Řešit SLAE $ \left\( \begin(zarovnáno) & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27; \\ & -3x_1-2x_2-2x_3-10x_4=1 \end(zarovnáno) \right.$ metodou Gauss-Jordan.

Napišme rozšířenou matici tohoto systému: $\widetilde(A)=\left(\begin(array) (cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end(pole) \vpravo)$.

Jako rozlišovací prvky vybereme diagonální prvky systémové matice: v prvním kroku vezmeme prvek prvního řádku, ve druhém kroku prvek druhého řádku atd.

První krok

Potřebujeme resetovat odpovídající prvky prvního sloupce. Vezměme prvek prvního řádku jako rozlišovací prvek, tzn. 3. Podle toho bude muset být první řádek rozdělen 3, aby se rozlišovací prvek rovnal jedné. A poté resetujte všechny prvky prvního sloupce, kromě povoleného:

$$ \left(\begin(pole)(cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\ \ -3 & -2 & -2 & -10 & 1\end(pole)\vpravo) \začátek(pole) (l) I:3\\ \phantom(0)\\\phantom(0)\\\ phantom(0)\end(pole) \rightarrow \left(\begin(pole)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end(pole)\vpravo) \začátek(pole) (l) \phantom(0) \\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end(pole) \rightarrow\\ \rightarrow\left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & - 5 & ​​​​-5\konec (pole)\vpravo). $$

Druhý krok

Pokračujeme k vynulování odpovídajících prvků druhého sloupce. Dohodli jsme se, že vezmeme prvek druhého řádku jako rozlišovací prvek, ale od té doby to nemůžeme udělat požadovaný prvek rovna nule. Závěr: vyměníme řádky. Prvního řádku se nelze dotknout, protože byl použit již v prvním kroku. Výběr není bohatý: buď prohodíme druhý a třetí řádek, nebo prohodíme čtvrtý a druhý. Protože čtvrtý řádek obsahuje (-1), nechť se „výměny“ účastní i čtvrtý řádek. Takže prohoďte druhý a čtvrtý řádek:

$$ \left(\begin(pole)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end(pole)\vpravo)\rightarrow \left(\begin(pole)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4 \end(pole)\vpravo) $$

Nyní je vše normální: prvek rozlišení je roven (-1). Stává se mimochodem, že změna polohy čar je nemožná, ale to si probereme v dalším příkladu č. 3. Prozatím vydělíme druhý řádek (-1) a poté vynulujeme prvky druhého sloupce. Upozorňujeme, že ve druhém sloupci je prvek umístěný ve čtvrtém řádku již roven nule, takže se čtvrtého řádku nedotkneme.

$$ \left(\begin(pole)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(pole)\vpravo) \začátek(pole) (l) \phantom(0)\\II:(-1) \\\phantom(0)\\\phantom(0)\end(pole) \rightarrow \left(\begin(pole)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(pole)\vpravo) \begin(pole) (l) I-1/3\cdot II\\ \phantom(0) \\III-2\cdot II\\\phantom(0)\end(array) \rightarrow\\ \rightarrow\left(\begin( pole)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\konec (pole)\vpravo). $$

Třetí krok

Začněme zpracovávat třetí sloupec. Dohodli jsme se, že jako rozlišovací prvek vezmeme diagonální prvky systémové matice. Pro třetí krok to znamená vybrat prvek umístěný na třetím řádku. Pokud však jednoduše vezmeme prvek 7 jako rozlišovací prvek, pak bude muset být celý třetí řádek vydělen 7. Zdá se mi, že dělení (-2) je jednodušší. Proto prohoďme třetí a čtvrtý řádek a pak se rozlišovacím prvkem stane (-2):

$$ \left(\begin(pole)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\konec (pole)\vpravo) \šipka vpravo \left(\začátek(pole)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end (pole)\vpravo) $$

Prvek rozlišení - (-2). Vydělte třetí řádek (-2) a vynulujte odpovídající prvky třetího sloupce:

$$ \left(\begin(pole)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & - 3 & -4\\ 0 & 0 & 7 & -9 & -25\end(pole)\vpravo) \začátek(pole) (l) \phantom(0)\\ \phantom(0) \\III:( -2)\\\phantom(0)\end(pole)\rightarrow \left(\begin(pole)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end (pole)\vpravo) \begin(pole) (l) I-2 /3\cdot III\\ \phantom(0) \\ \phantom(0)\\IV-7\cdot III\end(array)\rightarrow\\ \rightarrow\left(\begin(array)(cccc|c ) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & - 39\konec(pole)\vpravo). $$

Čtvrtý krok

Pojďme k vynulování čtvrtého sloupce. Rozlišovací prvek je umístěn na čtvrtém řádku a je roven číslu $-\frac(39)(2)$.

$$ \left(\begin(pole)(cccc|c) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2 \\ 0 & 0 & 0 & -39/2 & -39\end(pole)\vpravo) \begin(pole) (l) \phantom(0)\\ \phantom(0) \\ \phantom(0) \\IV:\left(-\frac(39)(2)\right) \end(pole)\rightarrow \left(\begin(pole)(cccc|c) 1 & 0 & 0 & -1 & -5 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end(pole)\vpravo) \begin(pole) (l ) I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom(0) \end(array)\rightarrow\\ \rightarrow\left(\begin(array)(cccc |c) 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end (pole)\vpravo). $$

Rozhodnutí je u konce. Odpověď je: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Kompletní řešení bez vysvětlení:

Odpovědět: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.

Příklad č. 3

Vyřešit SLAE $\left\(\začátek(zarovnáno) & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4 +14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_5=21x 9. \end(zarovnano)\vpravo.$ metodou Gauss-Jordan Pokud je systém nejistý, uveďte základní řešení.

Podobné příklady jsou diskutovány v tématu „Obecná a základní řešení SLAE“. V druhé části zmíněného tématu tento příkladřešeno pomocí Gaussovy metody. Vyřešíme to pomocí Gauss-Jordanovy metody. Řešení nebudeme rozebírat krok za krokem, protože to již bylo provedeno v předchozích příkladech.

$$ \left(\begin(pole)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end(pole)\right) \begin(pole) (l) \phantom(0) \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I \\ V+2\cdot I\\VI+4\cdot I \end(pole) \rightarrow \left(\begin(pole)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\ \\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end(pole)\vpravo) \začátek(pole) (l) \phantom(0) \\ II:5 \\ \ phantom(0)\\ \phantom(0)\\ \phantom(0) \\ \phantom(0)\end(array) \rightarrow \\ \left(\begin(array)(ccccc|c) 1 & - 2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end (pole)\vpravo) \ begin (pole) (l) I+2\cdot II \\ \phantom(0)\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \ end (pole) \rightarrow \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2 /5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & - 4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(pole)\vpravo). $$

Věřím, že jedna z provedených transformací stále vyžaduje vysvětlení: $IV:3$. Všechny prvky čtvrtého řádku jsou zcela dělitelné třemi, proto jsme čistě z důvodu zjednodušení rozdělili všechny prvky tohoto řádku na tři. Třetí řádek v transformované matici se stal nulou. Přeškrtneme nulový řádek:

$$ \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(pole)\vpravo) $$

Je čas, abychom přešli ke třetímu kroku, ve kterém by měly být resetovány prvky třetího sloupce. Diagonální prvek (třetí řádek) je však nulový. A změna polohy čar nic neudělá. První a druhý řádek jsme již použili, takže se jich nemůžeme dotknout. Ale nemá smysl se dotýkat čtvrtého a pátého řádku, protože problém s rozlišovacím prvkem rovným nule nezmizí.

V této situaci lze problém vyřešit extrémně jednoduchým způsobem. Nezvládneme třetí kolonu? Dobře, pojďme k číslu čtyři. Možná ve čtvrtém sloupci nebude prvek třetího řádku roven nule. Čtvrtá kolona však trpí stejným problémem jako třetí. Prvek třetího řádku ve čtvrtém sloupci je nula. A změna míst linek zase nic nedá. Nemůžeme zpracovat ani čtvrtý sloupec? Dobře, pojďme k číslu pět. Ale v pátém sloupci není prvek třetího řádku ani nulový. Rovná se jedné, což je docela dobré. Rozlišovací prvek v pátém sloupci je tedy roven 1. Rozlišovací prvek byl vybrán, takže provedeme další transformace Gauss-Jordanovy metody:

$$ \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(pole)\right) \begin(pole) (l) I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom(0)\\ IV+III\\ V+ 2 \cdot III \end(pole) \rightarrow \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1 / 5 & ​​2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end(pole)\right) \rightarrow \\ \rightarrow\left|\text(Odebrat nula řádků)\right|\rightarrow \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end (pole)\ vpravo )$$

Systémovou matici a rozšířenou systémovou matici jsme zredukovali na stupňovitou formu. Pořadí obou matic se rovnají $r=3$, tzn. musíte zvolit 3 základní proměnné. Počet neznámých je $n=5$, takže musíme vybrat $n-r=2$ volné proměnné. Od $ r< n$, то согласно следствию из теоремы Кронекера-Капелли данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим "ступеньки":

Na „stupních“ jsou prvky ze sloupců č. 1, č. 2, č. 5. V důsledku toho budou základní proměnné $x_1$, $x_2$, $x_5$. Volné proměnné budou $x_3$, $x_4$. Sloupce č. 3 a č. 4, odpovídající volným proměnným, přesuneme za řádek, přičemž samozřejmě nezapomeneme změnit jejich znaménka.

$$ \left(\begin(pole)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end(pole)\vpravo)\vpravo \left(\začátek(pole)(ccc|ccc) 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end (pole)\vpravo) . $$

Z poslední matice získáme obecné řešení: $\left\(\begin(zarovnáno) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5 )x_4 \\ & x_2=\frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \v R;\\ & x_4\; v R; \\ & x_5=4 \end(zarovnano)\vpravo.$.

$$ \left\(\begin(zarovnáno) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5);\\ & x_3=0;\\ & x_4= 0;\\ & x_5=4. \end(zarovnáno)\vpravo $$.

Problém je vyřešen, zbývá jen napsat odpověď.

Odpovědět: Společné rozhodnutí: $\left\(\begin(zarovnáno) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5)x_4;\\ & x_2=\ frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4 .\end(zarovnáno)\right.$, základní řešení: $\left\(\begin(zarovnáno) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5) ;\\ & x_3=0;\\ & x_4=0;\\ & x_5=4.

Podívejme se podrobně na to, jak se simplexové tabulky přepočítávají (na příkladu jedné iterace). Nechť je zde uvedena simplexní tabulka Obr. 1. Problém maximalizace účelové funkce je vyřešen. Sloupec rozlišení odpovídá proměnné x 2 a povolovací řetězec proměnné x 3(červená čísla), v jejich průsečíku je rozlišovací prvek (buňka s šedým pozadím). První věc, kterou musíme udělat, je vyměnit. Čára rozlišení označuje, která proměnná by měla být odvozena ze základu (v našem případě x 3), a sloupec rozlišení ukazuje, která proměnná by měla být zahrnuta do základu (v našem případě x 2). Na Obr.2 skutečnost výměny je zdůrazněna modrou čarou.

Nyní přepočítáme prvky v rozlišovací linii. Za tímto účelem jednoduše rozdělíme každý z nich na rozlišovací prvek (v našem příkladu 4 ). A vynulujeme všechny prvky sloupce rozlišení, kromě prvku v řádku rozlišení. (Dívej se Obr.2)

Obrázek 1

Zbývající buňky tabulky (kromě sloupce "Poměr") se přepočítají pomocí tzv. obdélníkové pravidlo, jehož význam je nejsnáze pochopitelný na příkladu. Předpokládejme, že potřebujeme přepočítat prvek, kterým kroužíme Obr. 1červený obrys. Mentálně z něj nakreslete svislou čáru a vodorovná čára až k průsečíku s rozlišovacím řádkem a rozlišovacím sloupcem. Prvky umístěné na křižovatkách jsou vyznačeny modrými obrysy (viz Obr. 1). Nová hodnota „červeného“ prvku se bude rovnat aktuální hodnotě prvku mínus součin „modrého“ prvku dělený rozlišovacím („šedým“) prvkem (viz. Obr. 1). to je: 18 - (64 * -1) / 4 = 34 , je tu známý" * “ ukazuje operaci násobení.
Novou hodnotu zapíšeme na stejné místo (viz Obr.2červený obrys).

Obrázek 2

Pomocí tohoto pravidla vyplňte vše prázdné prvky tabulky (kromě sloupce "Vztah") Viz Obr.3. Poté definujeme nový sloupec rozlišení. Abychom to udělali, analyzujme čáru "Q" a jelikož je naším úkolem maximum, najdeme v něm maximálně pozitivní prvek, určí sloupec rozlišení. V našem případě ano 3/2 . Všechny prvky sloupce rozlišení jsou zobrazeny červeným písmem (viz Obr.3). Pokud po další iteraci v řádku "Q" nebudou žádné pozitivní prvky - to znamená, že bylo dosaženo optimálního řešení, iterace se zastaví. Pokud by náš problém byl na minimu, pak by byl sloupec řešení určen minimálním záporným prvkem, a pokud by po další iteraci v řádku "Q" neexistují žádné negativní prvky, což znamená, že bylo dosaženo optimálního řešení.

Obrázek 3

Nyní vyplníme sloupec „Postoj“. Chcete-li to provést, musíte vydělit odpovídající (na stejném řádku) prvek sloupce „Rozhodnutí“ odpovídajícím prvkem sloupce rozlišení (viz Obr.3). Poznámka, Co tuto operaci držený jen pro ty pozitivní prvky rozlišovacího sloupce a řádku "Q" se této operace neúčastní. Pokud po nějaké iteraci nejsou ve sloupci rozlišení žádné kladné prvky, pak tento úkol je neřešitelný kvůli neohraničenosti účelové funkce, iterace se zastaví.

Po vyplnění sloupce "Vztah" nadefinujeme nový rozlišovací řádek. Je určeno minimálním prvkem ze sloupce "Relace". V našem případě ano 32 , všechny prvky řetězce rozlišení jsou zobrazeny červeným písmem (viz Obr.3). Zde končí další iterace, při další iteraci proměnná x 2 bude odstraněn ze základu (to nám říká nový rozlišovací řádek), jeho místo zaujme proměnná x 1(to nám říká nový sloupec rozlišení) a všechny výpočty se budou znovu opakovat.