El límite de una cantidad variable y sus propiedades. §2. Límite de valor variable. Importancia cultural y práctica general del paradigma de la continuidad y del cálculo diferencial e integral.
VARIABLES Y CONSTANTES
Como resultado de la medición cantidades fisicas(tiempo, área, volumen, masa, velocidad, etc.) se determinan sus valores numéricos. Las matemáticas se ocupan de cantidades, haciendo abstracción de su contenido específico. En lo que sigue, cuando hablemos de cantidades, nos referiremos a sus valores numéricos. En diversos fenómenos, algunas cantidades cambian, mientras que otras conservan su valor numérico. Por ejemplo, cuando un punto se mueve uniformemente, el tiempo y la distancia cambian, pero la velocidad permanece constante.
valor variable es una cantidad que toma diferentes valores numéricos. Una cantidad cuyos valores numéricos no cambian se llama constante. Las cantidades variables se indicarán con letras. x, y, z,…, constante - a, b, c,…
Tenga en cuenta que en matemáticas constante a menudo visto como caso especial una variable cuyos valores numéricos son todos iguales.
Cambiar área tamaño variable es el conjunto de todos los valores numéricos que acepta. El área de cambio puede constar de uno o más intervalos, o de un punto.
CANTIDAD VARIABLE PEDIDA. SECUENCIA NUMÉRICA
Diremos que la variable incógnita Hay variable ordenada, si se conoce el área de su cambio, y para cada uno de dos de sus valores se puede decir cuál es el anterior y cuál es el siguiente.
Un caso especial de cantidad variable ordenada es una cantidad variable cuyos valores forman secuencia numérica x 1 ,x 2 ,…,x n ,… Para tales valores en i< j, i, j Î N , significado xyo se considera antecedente, y xj– posterior independientemente de cuál de estos valores sea mayor. Por tanto, una secuencia numérica es una variable cuyos valores sucesivos pueden renumerarse. Denotaremos una secuencia numérica por . Los números individuales en una secuencia se llaman sus elementos.
Por ejemplo, la secuencia numérica está formada por las siguientes cantidades:
FUNCIÓN
Al estudiar diversos fenómenos naturales y resolver problemas técnicos y, en consecuencia, en matemáticas, es necesario considerar el cambio en una cantidad en función del cambio en otra. Por ejemplo, se sabe que el área de un círculo se expresa en términos de radio mediante la fórmula S = πr 2. Si radio r toma diferentes valores numéricos, entonces el área S también toma diferentes valores numéricos, es decir un cambio en una variable provoca un cambio en otra.
Si cada valor de variable incógnita pertenecer a una determinada región corresponde a una valor específico otra variable y, Eso y llamado función de la variable x. Escribiremos simbólicamente y=f(x). En este caso, la variable incógnita llamado variable independiente o argumento.
Registro y=C, Dónde do– constante, denota una función cuyo valor en cualquier valor incógnita uno y el mismo e igual do.
Múltiples significados incógnita, para lo cual se pueden determinar los valores de la función. y en concordancia con reglas f(x), llamado dominio de la función.
Tenga en cuenta que una secuencia numérica también es una función cuyo dominio de definición coincide con el conjunto números naturales.
Las funciones elementales básicas incluyen todas las funciones estudiadas en el curso de matemáticas de la escuela:
Función elemental es una función que se puede especificar mediante funciones elementales básicas y constantes usando un número finito de operaciones de suma, resta, multiplicación, división y tomando una función de una función.
EL CONCEPTO DE LÍMITE DE UNA SECUENCIA NUMÉRICA
En un curso posterior de matemáticas, el concepto de límite jugará un papel fundamental, ya que los conceptos básicos están directamente relacionados con él. análisis matemático– derivada, integral, etc.
Empecemos por el concepto de límite. secuencia numérica.
Número a llamado límite secuencias incógnita = {xn), si para un número positivo arbitrariamente predeterminado arbitrariamente pequeño ε existe tal número natural norte que delante de todos norte>norte la desigualdad |x n - a|< ε.
si el numero a hay un límite de secuencia incógnita = {xn), entonces dicen que xn se esfuerza por a y escribe.
Para formular esta definición en términos geométricos, introducimos el siguiente concepto.
Barrio del punto x 0 se llama intervalo arbitrario ( a, b), que contiene este punto dentro de sí mismo. La vecindad de un punto a menudo se considera x0, para lo cual x0 es el medio, entonces x0 llamado centro barrio, y el valor ( b–a)/2 – radio vecindario.
Entonces, descubramos qué significa geométricamente el concepto de límite de una secuencia numérica. Para hacer esto, escribimos la última desigualdad de la definición en la forma
Esta desigualdad significa que todos los elementos de la secuencia con números norte>norte debe estar en el intervalo (a – ε; a + ε).
Por lo tanto, un número constante a hay un límite para la secuencia numérica ( xn), si para cualquier vecindario pequeño centrado en el punto a radio ε (ε es la vecindad del punto a) existe tal elemento de la secuencia con número norte que todos los elementos siguientes estén numerados norte>norte se ubicará dentro de esta vecindad.
Ejemplos.
Hagamos algunos comentarios.
Nota 1. Obviamente, si todos los elementos de una secuencia numérica toman el mismo valor constante x norte = c, entonces el límite de esta secuencia será igual al más constante. De hecho, para cualquier ε la desigualdad | xn-c| = |cc| = 0 < ε.
Nota 2. De la definición de límite se deduce que una secuencia no puede tener dos límites. De hecho, supongamos que x norte → a y al mismo tiempo xn → b. Tome cualquiera y marque las vecindades de los puntos. a Y b radio ε (ver figura). Entonces, por definición de límite, todos los elementos de la secuencia, a partir de un cierto punto, deben ubicarse en una vecindad del punto. A, y en las proximidades del punto b, lo cual es imposible.
Nota 3. No debes pensar que toda secuencia numérica tiene un límite. Supongamos, por ejemplo, que una variable tome los valores 
. Es fácil ver que esta secuencia no tiende a ningún límite.
LÍMITE DE FUNCIÓN
Deja que la función y=f(x) definido en alguna vecindad del punto a. Supongamos que la variable independiente incógnita se acerca al número sin límite a. Esto significa que podemos dar incógnita valores lo más cercanos posible a a, pero no igual a. Lo denotaremos de esta manera. x → un. por tal incógnita Encontremos los valores correspondientes de la función. Puede suceder que los valores f(x) también acercarse a un cierto número sin límite b.Entonces dicen que el número b hay un límite de la función f(x) en x → un.
Introduzcamos una definición estricta del límite de una función.
Función y=f(x) tiende al límite b cuando x → a, si para cada número positivo ε, por pequeño que sea, es posible especificar un número positivo δ tal que para todo x ≠ a del dominio de definición de la función que satisface la desigualdad | x-a| < δ, имеет место неравенство |f(x)-b| < ε. Если b hay un límite de la función f(x) en x → un, luego escriben o f(x) → segundo en x → un.
Ilustremos esta definición con una gráfica de la función. Porque de la desigualdad | x-a| < δ должно следовать неравенство |f(x)-b| < ε, т.е. при incógnita Î ( a - δ, a+ δ) valores correspondientes de la función f(x) Î ( b - ε, b+ ε), entonces, tomando un ε > 0 arbitrario, podemos seleccionar un número δ tal que para todos los puntos incógnita, situada en δ – vecindad del punto a, los puntos correspondientes del gráfico de la función deben estar dentro de una franja de ancho 2ε delimitada por líneas rectas y = segundo– ε y y = segundo + ε.
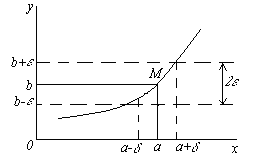
Es fácil ver que el límite de una función debe tener las mismas propiedades que el límite de una secuencia numérica, es decir, si en x → un La función tiene un límite, entonces es el único.
Ejemplos.
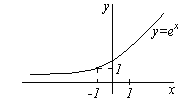
EL CONCEPTO DE LÍMITE DE UNA FUNCIÓN EN UN PUNTO INFINITAMENTE REMOTO
Hasta ahora hemos considerado los límites para el caso en que la variable incógnita se esforzó por alcanzar un cierto número constante.
Diremos que la variable x tiende al infinito, si para cada número positivo predeterminado METRO(puede ser tan grande como quieras) puedes especificar este valor x=x 0, a partir del cual todos los valores posteriores de la variable satisfarán la desigualdad |x|>M.
Por ejemplo, dejemos que la variable incógnita toma valores incógnita 1 = –1, x 2 = 2, x 3 = –3, …, x norte =(–1) nn,… Está claro que ésta es una variable infinitamente grande, ya que para todos METRO> 0 todos los valores de la variable, a partir de un determinado valor, serán mayores en valor absoluto METRO.
valor variable x → +∞, si por arbitrario METRO> 0 todos los valores posteriores de la variable, a partir de un determinado valor, satisfacen la desigualdad x > M.
Asimismo, incógnita→ – ∞, si por alguna METRO > 0 incógnita< -M .
Diremos que la función f(x) tiende al límite b en incógnita→ ∞, si para un número positivo pequeño y arbitrario ε se puede especificar dicho número positivo METRO, que para todos los valores incógnita, satisfaciendo la desigualdad |x|>M, la desigualdad | f(x)-b| < ε.
Designar.
Ejemplos.
CARACTERÍSTICAS INFINITAMENTE GRANDES
Anteriormente vimos casos donde la función f(x) Se esforzó por alcanzar un límite final. b en x → un o incógnita → ∞.
Consideremos ahora el caso en el que la función y=f(x) alguna forma de cambiar el argumento.
Función f(x) tiende al infinito como x → un, es decir. es infinitamente grande magnitud si para cualquier número METRO, no importa cuán grande sea, es posible encontrar un δ > 0 tal que para todos los valores incógnita≠a, cumpliendo la condición | x-a| < δ, имеет место неравенство |f(x)| > METRO.
Si f(x) tiende al infinito como x→a, luego escriben o f(x)→∞ en x→a.
Formule una definición similar para el caso en el que incógnita→∞.
Si f(x) tiende al infinito como x→a y al mismo tiempo acepta solo positivo o solo valores negativos, respectivamente escribe o .
Ejemplos.
CARACTERÍSTICAS LIMITADAS
Sea dada la función y=f(x), definido en algún conjunto D valores de argumento.
Función y=f(x) llamado limitado en un set D, si hay un número positivo METRO tal que para todos los valores incógnita del conjunto considerado, la desigualdad se cumple |f(x)|≤METRO. Si tal número METRO no existe, entonces la función f(x) llamado ilimitado en un set D.
Ejemplos.
- Función y=pecado incógnita, definido en -∞<incógnita<+∞, является ограниченной, так как при всех значениях incógnita|pecado incógnita|≤1 = METRO.
- Función y=x 2 +2 está limitado, por ejemplo, al segmento, ya que para todos incógnita de este segmento |f(x)| ≤ f(3) = 11.
- Considere la función y=ln incógnita en incógnitaО (0; 1). Esta función es ilimitada en el intervalo especificado, desde cuando incógnita→0 registro incógnita→-∞.
Función y=f(x) llamado acotado como x → a, si hay una vecindad centrada en el punto A, en el que la función es limitada.
Función y=f(x) llamado acotado como x→∞, si existe tal número norte> 0, que para todos los valores incógnita |x|>N, función f(x) limitado.
Establezcamos una conexión entre una función acotada y una función que tiene un límite.
Teorema 1. si y b es un número finito, entonces la función f(x) limitado cuando x→a.
Prueba. Porque , entonces para cualquier ε>0 hay un número δ>0 tal que para todos los valores incógnita, satisfaciendo la desigualdad |xa|<
δ, la desigualdad se cumple |f(x) –b|<
ε. Usando la propiedad del módulo |f(x) – b|≥|f(x)| - |b|, escribimos la última desigualdad en la forma |f(x)|<|b|+
ε. Así, si ponemos M=|b|+ε, entonces cuando x→a |f(x)|
Comentario. De la definición de función acotada se deduce que si , entonces es ilimitada. Sin embargo, lo contrario no es cierto: no función limitada Puede que no sea infinitamente grande. Da un ejemplo.
Teorema 2. Si, entonces la función y=1/f(x) limitado cuando x→a.
Prueba. De las condiciones del teorema se deduce que para arbitrario ε>0 en alguna vecindad del punto a tenemos |f(x) – b|<
ε. Porque |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, Eso |b| - |f(x)|<
ε. Por eso, |f(x)|>|b| -ε > 0. Por lo tanto 
LÍMITE. CONTINUIDAD DE FUNCIONES
VARIABLES Y CONSTANTES Como resultado de medir cantidades físicas (tiempo, área, volumen, masa, velocidad, etc.), se determinan sus valores numéricos. Las matemáticas se ocupan de cantidades, haciendo abstracción de su contenido específico. En lo que sigue, cuando hablemos de cantidades, nos referiremos a sus valores numéricos. En diversos fenómenos, algunas cantidades cambian, mientras que otras conservan su valor numérico. Por ejemplo, cuando un punto se mueve uniformemente, el tiempo y la distancia cambian, pero la velocidad permanece constante. valor variable es una cantidad que toma diferentes valores numéricos. Una cantidad cuyos valores numéricos no cambian se llama constante. Las cantidades variables se indicarán con letras. x, y, z,…, constante - a, b, c,… Tenga en cuenta que en matemáticas, un valor constante a menudo se considera un caso especial de una variable en la que todos los valores numéricos son iguales. Cambiar área Una variable es el conjunto de todos los valores numéricos que acepta. El área de cambio puede constar de uno o más intervalos, o de un punto. CANTIDAD VARIABLE PEDIDA. SECUENCIA NUMÉRICA Diremos que la variable incógnita Hay variable ordenada, si se conoce el área de su cambio, y para cada uno de dos de sus valores se puede decir cuál es el anterior y cuál es el siguiente. Un caso especial de cantidad variable ordenada es una cantidad variable cuyos valores forman secuencia numérica incógnita 1 ,incógnita 2 ,…,incógnita norte ,… Para tales valores en i< j, i, j Î N , significado incógnita i se considera antecedente, y incógnita j– posterior independientemente de cuál de estos valores sea mayor. Por tanto, una secuencia numérica es una variable cuyos valores sucesivos pueden renumerarse. Denotaremos una secuencia numérica por . Los números individuales en una secuencia se llaman sus elementos. Por ejemplo, la secuencia numérica está formada por las siguientes cantidades:
FUNCIÓN Al estudiar diversos fenómenos naturales y resolver problemas técnicos y, en consecuencia, en matemáticas, es necesario considerar el cambio en una cantidad en función del cambio en otra. Por ejemplo, se sabe que el área de un círculo se expresa en términos de radio mediante la fórmula S = πr 2
. Si radio r toma diferentes valores numéricos, entonces el área S también toma diferentes valores numéricos, es decir un cambio en una variable provoca un cambio en otra. Si cada valor de variable incógnita pertenecer a un área determinada corresponde a un valor específico de otra variable y, Eso y llamado función de la variable x. Escribiremos simbólicamente y=f(x). En este caso, la variable incógnita llamado variable independiente o argumento. Registro y=C, Dónde do– constante, denota una función cuyo valor en cualquier valor incógnita uno y el mismo e igual do. Múltiples significados incógnita, para lo cual se pueden determinar los valores de la función. y en concordancia con reglas f(x), llamado dominio de la función. Tenga en cuenta que una secuencia numérica también es una función cuyo dominio de definición coincide con el conjunto de los números naturales. Las funciones elementales básicas incluyen todas las funciones estudiadas en el curso de matemáticas de la escuela: Función elemental es una función que se puede especificar mediante funciones elementales básicas y constantes usando un número finito de operaciones de suma, resta, multiplicación, división y tomando una función de una función. EL CONCEPTO DE LÍMITE DE UNA SECUENCIA NUMÉRICA En un curso posterior de matemáticas, el concepto de límite jugará un papel fundamental, ya que los conceptos básicos del análisis matemático están directamente relacionados con él: derivada, integral, etc. Comencemos con el concepto de límite de una secuencia numérica. Número a llamado límite secuencias incógnita = {incógnita norte), si para un número positivo arbitrariamente predeterminado arbitrariamente pequeño ε existe tal número natural norte que delante de todos norte>norte la desigualdad |x n - a|< ε. Если число a hay un límite de secuencia incógnita = {incógnita norte), entonces dicen que incógnita norte se esfuerza por a y escribe. Para formular esta definición en términos geométricos, introducimos el siguiente concepto. Barrio del punto x 0
se llama intervalo arbitrario ( a, b), que contiene este punto dentro de sí mismo. La vecindad de un punto a menudo se considera incógnita 0
, para lo cual incógnita 0
es el medio, entonces incógnita 0
llamado centro barrio, y el valor ( b–a)/2 – radio vecindario. Entonces, descubramos qué significa geométricamente el concepto de límite de una secuencia numérica. Para hacer esto, escribimos la última desigualdad de la definición en la forma Esta desigualdad significa que todos los elementos de la secuencia con números norte>norte debe estar en el intervalo (a – ε; a + ε). CON 
por lo tanto, un número constante a hay un límite para la secuencia numérica ( incógnita norte), si para cualquier vecindario pequeño centrado en el punto a radio ε (ε es la vecindad del punto a) existe tal elemento de la secuencia con número norte que todos los elementos siguientes estén numerados norte>norte se ubicará dentro de esta vecindad. Ejemplos.
- deja que la variable incógnita toma valores secuencialmente
, entonces para satisfacer la relación |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве norte cualquier número natural que satisfaga la desigualdad, obtenemos lo que necesitamos. Entonces, si tomamos, por ejemplo, entonces, poniendo norte= 6, para todos norte>6 tendremos 
. Tomemos un ε > 0 arbitrario. Consideremos . Entonces, si o, es decir . Por tanto, elegimos cualquier número natural que satisfaga la desigualdad. Hagamos algunos comentarios. Nota 1. Obviamente, si todos los elementos de una secuencia numérica toman el mismo valor constante incógnita norte =c, entonces el límite de esta secuencia será igual al más constante. De hecho, para cualquier ε la desigualdad | incógnita norte -c| = |cc| = 0 < ε. z 
Nota 2. De la definición de límite se deduce que una secuencia no puede tener dos límites. De hecho, supongamos que incógnita norte →a y al mismo tiempo incógnita norte →b. Tome cualquiera y marque las vecindades de los puntos. a Y b radio ε (ver figura). Entonces, por definición de límite, todos los elementos de la secuencia, a partir de un cierto punto, deben ubicarse en una vecindad del punto. A, y en las proximidades del punto b, lo cual es imposible. Nota 3. No debes pensar que toda secuencia numérica tiene un límite. Supongamos, por ejemplo, que una variable tome los valores 
. Es fácil ver que esta secuencia no tiende a ningún límite. | LÍMITE DE FUNCIÓN Deja que la función y=f(x) definido en alguna vecindad del punto a. Supongamos que la variable independiente incógnita se acerca al número sin límite a. Esto significa que podemos dar incógnita valores lo más cercanos posible a a, pero no igual a. Lo denotaremos de esta manera. x → un. por tal incógnita Encontremos los valores correspondientes de la función. Puede suceder que los valores f(x) también acercarse a un cierto número sin límite b.Entonces dicen que el número b hay un límite de la función f(x) en x → un. Introduzcamos una definición estricta del límite de una función. Función y=f(x) tiende al límite b cuando x → a, si para cada número positivo ε, por pequeño que sea, se puede especificar un número positivo δ tal que para todo x ≠ a del dominio de definición de la función | x-a| < δ, имеет место неравенство |f(x)-b| < ε. Если b hay un límite de la función f(x) en x → un, luego escriben o f(x) → segundo en x → un. Ilustremos esta definición con una gráfica de la función. Porque de la desigualdad | x-a| < δ должно следовать неравенство |f(x)-b| < ε, т.е. при incógnita Î ( a - δ, a+ δ) valores correspondientes de la función f(x) Î ( b - ε, b+ ε), entonces, tomando un ε > 0 arbitrario, podemos seleccionar un número δ tal que para todos los puntos incógnita, situada en δ – vecindad del punto a, los puntos correspondientes del gráfico de la función deben estar dentro de una franja de ancho 2ε delimitada por líneas rectas y = segundo– ε y y = segundo+ε. Es fácil ver que el límite de una función debe tener las mismas propiedades que el límite de una secuencia numérica, es decir, si en x → un La función tiene un límite, entonces es el único. Ejemplos. Usando un gráfico función dada, es fácil de notar. |
|
EL CONCEPTO DE LÍMITE DE FUNCIÓN EN UN PUNTO INFINITAMENTE REMOTO Hasta ahora hemos considerado los límites para el caso en que la variable incógnita se esforzó por alcanzar un cierto número constante. Diremos que la variable x tiende al infinito, si para cada número positivo predeterminado METRO(puede ser tan grande como quieras) puedes especificar este valor x=x 0
, a partir del cual todos los valores posteriores de la variable satisfarán la desigualdad |x|>M. Por ejemplo, dejemos que la variable incógnita toma valores incógnita 1 = –1, x 2 =
2, x 3 = –3, …, x norte =(–1) norte norte,... Está claro que ésta es una variable infinitamente grande, ya que para todos METRO> 0 todos los valores de la variable, a partir de un determinado valor, serán mayores en valor absoluto METRO. valor variable x → +∞, si por arbitrario METRO> 0 todos los valores posteriores de la variable, a partir de un determinado valor, satisfacen la desigualdad x > M. Asimismo, incógnita→ – ∞, si por alguna METRO > 0 incógnita< -M
. Diremos que la función f(x) tiende al límite b en incógnita→ ∞, si para un número positivo pequeño y arbitrario ε se puede especificar dicho número positivo METRO, que para todos los valores incógnita, satisfaciendo la desigualdad |x|>M, la desigualdad | f(x)-b| < ε. Обозначают . Ejemplos. norte 
Ya es posible demostrar que para ε arbitrario la desigualdad se satisfará tan pronto como |x|>M, y el número METRO debe estar determinado por la elección de ε. La desigualdad escrita es equivalente a la siguiente, que se cumplirá si |x|> 1/ε=M. Esto significa que (ver figura). CARACTERÍSTICAS INFINITAMENTE GRANDES Anteriormente vimos casos donde la función f(x) Se esforzó por alcanzar un límite final. b en x → un o incógnita→ ∞. Consideremos ahora el caso en el que la función y=f(x) alguna forma de cambiar el argumento. Función f(x) tiende al infinito como x → un, es decir. es infinitamente grande magnitud si para cualquier número METRO, no importa cuán grande sea, es posible encontrar un δ > 0 tal que para todos los valores incógnita≠a, cumpliendo la condición | x-a| < δ, имеет место неравенство |f(x)| > METRO. Si f(x) tiende al infinito como x→a, luego escriben o f(x)→∞ en x→a. Formule una definición similar para el caso en el que incógnita→∞. Si f(x) tiende al infinito como x→a y al mismo tiempo toma sólo valores positivos o sólo negativos, en consecuencia escriben o . Ejemplos. 
CARACTERÍSTICAS LIMITADAS Sea dada la función y=f(x), definido en algún conjunto D valores de argumento. Función y=f(x) llamado limitado en un set D, si hay un número positivo METRO tal que para todos los valores incógnita del conjunto considerado, la desigualdad se cumple |f(x)|≤METRO. Si tal número METRO no existe, entonces la función f(x) llamado ilimitado en un set D. Ejemplos.
- Función y=pecado incógnita, definido en -∞<incógnita<+∞, является ограниченной, так как при всех значениях incógnita|pecado incógnita|≤1 = METRO. Función y=x 2 +2 está limitado, por ejemplo, al segmento, ya que para todos incógnita de este segmento |f(x)| ≤ f(3) = 11. Considere la función y=ln incógnita en incógnitaО (0; 1). Esta función es ilimitada en el intervalo especificado, desde cuando incógnita→0 registro incógnita→-∞.
. FUNCIONES INFINITAMENTE GRANDES E INFINITAS PEQUEÑAS
INFINITAS PEQUEÑAS FUNCIONES Y SUS PROPIEDADES BÁSICAS Función y=f(x) llamado infinitesimal en x→a o cuando incógnita→∞, si o , es decir Una función infinitesimal es una función cuyo límite en un punto dado es cero. PAG
ejemplos. 
Establezcamos la siguiente relación importante: Teorema. Si la función y=f(x) representable con x→a como suma de un número constante b y sin cesar tamaño pequeño α(x): f (x)=b+ α(x) Eso . Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a. Prueba. Consideremos las propiedades básicas de las funciones infinitesimales. Teorema 1. La suma algebraica de dos, tres y en general cualquier número finito de infinitesimales es una función infinitesimal. Prueba. Demos una prueba para dos términos. Dejar f(x)=α(x)+β(x), dónde y . Necesitamos demostrar que para ε arbitrariamente pequeño >
0 encontrado δ>
0, tal que para incógnita, satisfaciendo la desigualdad |x – a|<δ
, se ejecuta |f(x)|<
ε. Entonces, arreglemos un número arbitrario ε >
0. Dado que según las condiciones del teorema a(x) es una función infinitesimal, entonces existe tal δ 1 >
0, que es |x – a|<
δ 1 tenemos |α(x)|<
ε /
2.
Asimismo, desde β(x) es infinitesimal, entonces existe tal δ 2 >
0, que es |x – a|<
δ 2 tenemos | β(x)|<
ε /
2.
tomemos δ=mín(δ 1 ,
δ2 }
.Luego en las proximidades del punto a radio δ
cada una de las desigualdades será satisfecha |α(x)|<
ε /
2 y | β(x)|<
ε /
2.
Por lo tanto, en este barrio habrá |f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|<
ε /2 +
ε /2=
ε, es decir |f(x)|<
ε, que es lo que había que demostrar. Teorema 2. Producto de una función infinitesimal hacha) para una función limitada f(x) en x→a(o cuando x→∞) es una función infinitesimal. Prueba. Desde la función f(x) es limitado, entonces hay un número METRO tal que para todos los valores incógnita desde algún barrio de un punto a|f(x)|≤M. Es más, desde hacha) es una función infinitesimal en x→a, entonces para un ε arbitrario >
0 hay una vecindad del punto a, en el que la desigualdad se mantendrá |α(x)|<
ε /METRO. Luego, en el más pequeño de estos barrios tenemos | αf|<
ε /METRO= ε. Y esto significa que af– infinitesimal. para la ocasión x→∞ la prueba se realiza de manera similar. Del teorema probado se sigue: Corolario 1. Si y, entonces. Corolario 2. si y c= constante, entonces. Teorema 3. Razón de una función infinitesimal a(x) por función f(x), cuyo límite es distinto de cero, es una función infinitesimal. Prueba. Dejar 
. Entonces 1 /f(x) hay una función limitada. Por lo tanto la fracción 
es el producto de una función infinitesimal y una función acotada, es decir la función es infinitesimal. 1. Importancia cultural y práctica general del paradigma de la continuidad y del cálculo diferencial e integral
AbstractoApéndice 1 Elementos de la aplicación de las matemáticas en la investigación socioeconómica y sociogerencial y en la práctica empresarial moderna: posibles temas aplicados para resúmenes.
- Documento
Este capítulo describe los nombres válidos de variables y funciones de Mathcad, los gustos de variables predefinidos y las representaciones numéricas de Mathcad. números complejos con la misma facilidad que con los reales.
"Funciones y gráficas"
AbstractoMe gustaría saber más sobre qué es una función y gráficas de funciones. A partir del séptimo grado estudiamos álgebra según el programa A.G. Mordkovich. Creo que el concepto dependencia funcional Es uno de los principios centrales de las matemáticas e impregna todas sus aplicaciones.
Una breve descripción general y una guía de referencia. El libro es la primera revisión y guía de referencia sobre física virtual de este tipo y está destinado a una amplia gama de lectores interesados en los problemas de la ciencia en general y de la física en particular.
LibroEl libro es la primera revisión y guía de referencia sobre física virtual de este tipo y está destinado a amplio círculo Lectores interesados en problemas de la Ciencia en general y de la Física en particular.
Programa de pruebas de acceso a programas de maestría en la dirección 010200. 68 Matemáticas. Matemáticas aplicadas "Análisis matemático"
ProgramaLímite de secuencia numérica. Propiedades básicas: unicidad del límite; secuencia convergente limitada; convergencia de una subsecuencia de una secuencia convergente.
Sea x una variable ordenada (por ejemplo, una secuencia numérica).
Definición.
numero constantease llama límite de una variable x si cualquier número positivo arbitrariamente pequeño no lo tomamos, puede especificar un valor para la variable x tal que todos los valores posteriores de la variable satisfagan la desigualdad incógnita-A .
Simbólicamente, esto se escribe xa o limx=a (del latín limes - límite).
Geométricamente esta definición significa que no importa qué pequeña - vecindad del punto a tomemos, todos los valores posteriores de x después de un cierto punto se encontrarán en esta vecindad.
Del dibujo se desprende claramente que la desigualdad 
significa que la distancia del punto x a a es menor que . Y este es el interior del barrio. El punto x obviamente también satisface la doble desigualdad a- 
y estos son equivalentes.
ACERCA DE 
definición: Para una secuencia numérica (x n) a es el límite si 
puede especificar un número N tal que para todos 
Para los miembros de la secuencia, todos los valores x N , x N +1 y más se encuentran dentro 
-el barrio es imprescindible.
Una variable x, cuyos valores forman la secuencia numérica x 1,x 2,…,x n, a menudo se escribe como miembro de la secuencia x=x n o (x n). Por ejemplo, (1/n). Esta es una cantidad o secuencia variable con un término común x n =1/n: 1,1/2,1/3…
Ejemplo: Dejemos que la variable x tome valores secuenciales: x 1 =2/1, x 2 =3/2, x 3 =4/3, …,x n =(n+1)/n,… es decir formar una secuencia numérica. Probemos que 
.
tomemos 
.
. Tan pronto como el número sea 
, lo tomaremos como N. Entonces la desigualdad se mantendrá para 
. Pero luego todo está demostrado.
Teorema 1: el límite de un valor constante es igual a esta constante. Prueba: Un valor constante es un caso especial de una variable: todos sus valores =c: x=c/ Pero entonces limc=c.
Teorema 2: La variable x no puede tener dos límites.
Prueba: Digamos limx=a y limx=b. Entonces 
Y 
después de algún valorx. Pero entonces
Porque 
arbitrariamente pequeña, entonces la desigualdad sólo es posible cuando a = b
Nota: La variable puede no tener límite: x=x n =(-1) n =-1,+1,-1,+1. La distancia a cualquier punto a desde sus valores –1,+1 no puede ser menor que 1/2 
(-1) n no tiene límite.
Supusimos que a era un número. Pero la variable x también puede tender al infinito.
Definición: La variable x tiende a infinito si por 
a partir de un cierto valor x peso, los valores restantes satisfacen la desigualdad 
. Variablex tiende a 
, si bajo las mismas condiciones la desigualdad x>M y k - 
, si en las mismas condiciones la desigualdad x<-M.
Если переменная X
стремится к бесконечности, то её называют
infinitamente grande y escribe 
Ejemplo: x=x norte =norte 2 . tomemos 
>0. n 2 >M debe cumplirse. n> 
. Tan pronto como n satisface esta desigualdad, entonces para todo x n = n 2 se satisface la desigualdad. Entonces n 2 
, o mejor dicho n 2 
.
§3. Límite de función.
Supondremos que el argumento x de la función y=f(x) tiende a x 0 o .
Consideremos el comportamiento de la función y en estos casos.
Definición.
Dejemos que la función y=f(x) se defina en una determinada vecindad del punto x 0. Un número A se llama límite de una función para xx 0 si para cualquier , por pequeño que sea, se puede especificar un número tal que para todo xx 0 y que satisfaga la desigualdad x-x 0 se cumple la desigualdad f (x)-A.
Si A es el límite de la función f(x), entonces escriben 
orf(x)A en xx 0.
ACERCA DE 
La definición se puede ilustrar de esta manera. geométricamente.
Si A es el límite de f(x) para xx 0, entonces tomando cualquier vecindad del punto A, siempre podemos indicar tal vecindad del punto x 0 que para todo x de esta vecindad del valor de la función f(x) están distantes de A no más que , es decir caerá en el vecindario seleccionado del punto A, o, de todos modos, la parte del gráfico correspondiente a los puntos x del vecindario se encuentra completamente en una franja de ancho 2.
Se puede observar que cuanto menor es , menor debe ser .
Definición.
Deje que el argumento x tienda al punto x 0, tomando todo el tiempo los valores xx 0 xx 0 Entonces el número A 1 (A 2), al que tiende la función f(x), se llama límite de la función f(x) en el punto x 0 hacia la derecha (izquierda) o hacia la derecha (zurdo).
Se escribe: lim x x0+0 f(x)=A 1, (lim x x0-0 f(x)=A 2).
Se puede demostrar que si existe el límite lim x x0 f(x) = A, entonces ambos límites unilaterales existen en este punto y son iguales, A 1 = A 2 = A. A la inversa: si hay límites unilaterales y son iguales, entonces hay un límite general. Si al menos uno no existe o no son iguales, entonces el límite de la función no existe.
Ejemplo.
Demuestre que f(x)=3x-2 tiene un límite en x1 igual a 1.
Cualquiera , х 3.
Como puedes tomar cualquier número positivo /3; 0</3.
Demostraron que para cualquier basta con tomar /3 para que de 0х f(x)-1, pero esto significa que lim X (3x-2)=1.
Definición.
h 
El número A se llama límite de la función y=f(x) para x si para cualquier (por pequeño que sea) se puede especificar un número positivo P tal que para todos los valores de x que satisfacen la desigualdad xP la desigualdad f(x)-A.
Escribe lim x f(x)=A.
Geométricamente, esto significa que para cualquier la gráfica de la función para xp y x-p se ubica en una franja de ancho 2.
Ejemplo.
f(x)=1/x para x, f(x)0.
Cualquiera que sea el valor de 0, la gráfica de la función para xP y x-P se ubicará en una franja de ancho 2.
1/х, 1/х, x1/, Р=1/.
Definido de manera similar 
f(x)=A 1 y 
f(x)=A2. En el primer caso, se debe satisfacer la desigualdad f(x)-A 1 para xP, en el segundo caso f(x)-A 2 para x-P (P0 .
Entonces, 
1/x=0, y 
1/x=0. Su igualdad nos permite considerar el límite general. 
1/x=0.
2 Límite de valor variable. Cantidades infinitamente pequeñas e infinitamente grandes, la conexión entre ellas.
El límite de una variable en un punto determinado es numéricamente igual a ese punto. limx(xàa) = a
La función se llama infinitesimal en el punto donde xàa si yà0. limf(x)_(xàa) = 0
Se dice que la función es infinitamente grande en el punto donde xàa si yà0. limf(x)_(xàa) =<><>
Relación entre cantidades:
Si y=Ф(х) es infinitesimal, entonces 1/ф(х) es infinitamente enfermo
3 Infinitesimales, sus propiedades básicas.
La suma de un número finito de cantidades infinitesimales es una cantidad infinitesimal.
El producto de una función finita y una cantidad infinitesimal es una cantidad infinitesimal.
Una función en el punto a tiene un límite finito si y sólo si f(x) = A + U(x), donde U(x) es una cantidad infinitesimal. Alternativamente, esto se puede escribir como f(x) – A à 0.
Comparación de funciones infinitesimales:
Si el límite de proporción de un b.m. a otro b.m. es igual a cero, entonces el b.m. que estaba en el numerador. orden superior más blanco. Si este límite es igual al infinito, entonces viceversa.
Y si el límite de su proporción es igual a un cierto número, entonces estos b.m. mismo orden.
Si el límite es 1, entonces estos dos b.m. son equivalentes.
Teorema 1: el producto de infinitesimales es un infinitesimal de orden superior a cada uno de ellos.
AOD . La función a(x) se llama b/m si su límite en este tipo es igual a 0. De esta definición se deduce la siguiente propiedad de las funciones b/m:
a) La suma algebraica y el producto de funciones b/m son funciones b/m.
b) El producto de una función b/m y una función limitada es una función b/m, es decir si a(x)®0 para x®x0, y f(x) está definida y limitada ($ C:½j(x)½£C) => j(x)a(x)®0 para x®x0
Para distinguir los vehículos por su velocidad de aproximación a 0, se introduce lo siguiente. concepto:
1) Si la relación de 2 b/m a(x)/b(x)®0 en x®x0 entonces dicen que b/m a tiene un orden de pequeñez mayor que b.
2) Si a(x)/b(x)®A¹0 para x®x0 (número A), entonces a(x) y b(x) se denominan b/m del mismo orden.
3) si a(x)/b(x)®1, entonces se dice que a(x) y b(x) son b/m equivalentes (a(x)~b(x)), para x®x0.
4) Si a(x)/b^n(x)®А¹0, entonces a(x) se llama b/m de enésimo orden con respecto a b(x).
Definiciones similares para los casos: x®x0-, x®x0+, x®-¥, x®+¥ y x®¥.
4 Límite de función. Teoremas básicos sobre límites.
Definición límite: sea φ(x) una función definida en el conjunto X, y a sea el punto límite de este conjunto. El número A se llama límite funciona para x à a si y sólo si para cualquier e existe una vecindad del punto a tal que |ф(x) – a|< |е|
De otra manera, esto se escribe como f(x) à A para x à a
Teorema 1: Si cada término de una suma algebraica de un número finito de funciones tiene un límite cuando x tiende a a, entonces el límite de esta suma algebraica en x es el mismo. k a existe y es igual a la misma suma algebraica de los límites de los términos.
Prueba: representamos una función como la suma de su límite y un infinitesimal, sumamos funciones e infinitesimales. Resulta que la suma de las funciones difiere de la suma de los límites en una cantidad infinitesimal, lo que significa que este es el límite.
Consecuencia: Una función solo puede tener un límite en el nivel x. a un. Probado por contradicción. Resulta que la diferencia entre las funciones originales tiende a la diferencia entre sus límites, es decir, cero tiende a la diferencia entre los límites, y dado que el límite de una función constante es igual a la función misma y es único, entonces obtenemos que la diferencia del límite es igual a 0, es decir, los límites son iguales.
Teorema 2: Si cada uno de los factores del producto de un número finito de funciones tiene un límite en x à a, entonces el límite del producto en x a es igual al producto de los límites de los factores.
Evidencia: Se considera el producto de dos factores.
De las diversas formas en que se comportan las variables, la más importante es aquella en la que la variable tiende a un cierto límite. En este caso, los valores que toma la variable incógnita, acercarse arbitrariamente a algún número constante a- el límite de esta variable. Dicen que una variable tiende a acercarse a un número constante sin límite. A(hasta tu límite). Demos la definición correspondiente con más detalle.
La variable x tiende al límite a (a - número constante) si el valor absoluto la diferencia entre x y a se vuelve arbitrariamente pequeña en el proceso de cambiar la variable.
La misma definición se puede decir en otras palabras.
Definición.El número constante a se llamalímite variablex si - el valor absoluto de la diferencia entre x y a se vuelve arbitrariamente pequeño en el proceso de cambio de la variable x.
El hecho de que el número A, es el límite de la variable, escrito de la siguiente manera:
( - las primeras letras de la palabra limas - límite) o incógnita-> un
Aclaremos qué debe entenderse por las palabras "la cantidad se vuelve arbitrariamente pequeña" en la definición del límite. Establezcamos un número positivo arbitrario, entonces si, a partir de un momento determinado en el cambio de la variable INCÓGNITA, los valores serán y serán menores que esto 
.
La variable tiende al límite si es positiva. a partir de un determinado momento en el cambio de la variable, la desigualdad se satisface 
.
La definición del límite tiene un significado geométrico simple: la desigualdad significa que está ubicado en la vecindad del punto, es decir en el intervalo (Fig. 26). Así, definir el límite en forma geométrica: un número es el límite de una variable si es para alguna (arbitrariamente pequeña)-barrio de un punto puede especificar el momento en el que se cambia una variable a partir del cual todos sus valores
caer en el vecindario indicado del punto a.
Es necesario imaginar el proceso de acercarse al límite en dinámica. Tomó algunos - vecindad de un punto a; comenzando en algún momento del cambio , todos los valores caen dentro de este vecindario. Ahora echemos un vistazo más de cerca - vecindad de un punto a; a partir de algún momento (más lejano en comparación con el primero) del cambio , todos sus valores caerán en - vecindad de un punto A etc. (Figura 1).
 |
|||
 |
|||
Habiendo introducido la definición del límite de un valor variable, intentamos discutirlo y descifrarlo en detalle. Sin embargo, en esta definición quedó sin revelar un detalle muy significativo; ¿Qué debe entenderse por las palabras “a partir de un momento determinado en el cambio de una variable”? Esto queda claro cuando el proceso de cambio de una variable se produce a lo largo del tiempo: a partir de un determinado momento (tiempo). Pero no siempre se trata de cantidades variables cuyo cambio se produce con el tiempo. ¿Qué hacer en estos casos? La solución es descifrar este lugar en definición general limitar una variable de forma específica para cada tipo de variable: a su manera para secuencias, a su manera para funciones, etc.
Límite de consistencia. En primer lugar, debemos recordar la definición de secuencia: si todos los valores tomados por una variable incógnita, se puede numerar utilizando todos los números naturales posibles x), x 2,...x n,..., y el valor con un número mayor se toma después del valor con un número menor, entonces se dice que la variable es incógnita recorre una secuencia de valores x x, x 2,... x n...; o simplemente que hay una secuencia (una secuencia numérica).
Definición. secuencia numérica se llama función real de un argumento natural, es decir, una función cuyo = norte Y EÌR.
Se denota con el símbolo , donde , o en resumen, . Un número que depende de n se llama n – ésimo miembro de la secuencia. Ordenando los valores de la secuencia en orden numérico, encontramos que la secuencia se puede identificar con un conjunto contable. números reales, es decir.
Ejemplos:
a) La secuencia es constante y consta de números iguales (unidades): ;
b) 
. para ella
GRAMO) 
.
Para secuencias, contenidas en la definición general del límite de una variable, la afirmación “a partir de un momento determinado en el cambio " debe significar "a partir de un número determinado", ya que los miembros con números más altos siguen (por definición de secuencia) al miembro con números más bajos. Entonces obtenemos la siguiente definición del límite de una secuencia:
Definición. Número A llamado límite secuencias, si para cualquier número hay un número tal que todos los números satisfacen la desigualdad.
Designación correspondiente
La desigualdad también se puede escribir en la forma 
o . Estos registros enfatizan que el valor xn se vuelve lo más indistinguible posible de a, cuando el número de socios aumente sin límite. Geométricamente, la definición del límite de una secuencia significa lo siguiente: para arbitrariamente pequeño -barrio del número A hay un número N tal que todos los términos de la secuencia con mayor que N, los números caen en esta vecindad, Sólo un número finito de términos iniciales de la secuencia están fuera de la vecindad (Fig. 2). ¿Son todos o algunos de los miembros? .
x 1 x 2 x N +1 a x N +2 x N x 3
El número en nuestra definición depende de : norte= NORTE(). Como se mencionó anteriormente, la definición del límite debe entenderse en el desarrollo, en la dinámica, en el movimiento: si tomamos otro valor menor para , por ejemplo, entonces, en términos generales, existe otro número norte x > norte, tal que la desigualdad , está satisfecho por todos .
Anotaremos la definición de límite utilizando símbolos lógicos (cuantificadores). Definir el límite de una secuencia usando cuantificadores se ve así.
