Limita proměnné hodnoty a její vlastnosti. §2. Limit proměnné hodnoty. Obecný kulturní a praktický význam paradigmatu kontinuity a diferenciálního a integrálního počtu
PROMĚNNÉ A KONSTANTY
Jako výsledek měření fyzikální veličiny(čas, plocha, objem, hmotnost, rychlost atd.) jsou určeny jejich číselné hodnoty. Matematika se zabývá veličinami, abstrahuje od jejich konkrétního obsahu. V následujícím, když mluvíme o veličinách, budeme mít na mysli jejich číselné hodnoty. Při různých jevech se některé veličiny mění, jiné si zachovávají svou číselnou hodnotu. Například, když se bod pohybuje rovnoměrně, čas a vzdálenost se mění, ale rychlost zůstává konstantní.
Proměnná hodnota je veličina, která nabývá různých číselných hodnot. Volá se veličina, jejíž číselné hodnoty se nemění konstantní. Variabilní množství budou označena písmeny x, y, z…, konstantní - a, b, c,…
Všimněte si, že v matematice konstantníčasto viděn jako speciální případ proměnná, jejíž číselné hodnoty jsou všechny stejné.
Změnit oblast variabilní velikost je množina všech číselných hodnot, které přijímá. Oblast změny se může skládat z jednoho nebo více intervalů nebo jednoho bodu.
OBJEDNÁVANÉ VARIABILNÍ MNOŽSTVÍ. ČÍSELNÁ POŘADÍ
Řekneme, že proměnná X Tady je objednaná proměnná, pokud je známa oblast jeho změny a pro každou z jeho dvou hodnot lze říci, která z nich je předchozí a která je následující.
Zvláštním případem objednané proměnné veličiny je proměnná veličina, jejíž hodnoty tvoří číselná řada x 1, x 2,…, x n,… Pro takové hodnoty při i< j, i, j Î N , význam x i je považován za předchůdce a x j– následující bez ohledu na to, která z těchto hodnot je větší. Číselná posloupnost je tedy proměnná, jejíž po sobě jdoucí hodnoty lze přečíslovat. Číselnou posloupnost budeme označovat . Jednotlivá čísla v posloupnosti se nazývají jeho Prvky.
Například číselná posloupnost je tvořena následujícími veličinami:
FUNKCE
Při studiu různých přírodních jevů a řešení technických problémů a následně i v matematice je nutné uvažovat o změně jedné veličiny v závislosti na změně jiné. Například je známo, že plocha kruhu je vyjádřena jako poloměr vzorcem S = πr 2. Pokud poloměr r nabývá různých číselných hodnot, pak plochy S nabývá také různých číselných hodnot, tzn. změna jedné proměnné způsobí změnu jiné.
Pokud každá proměnná hodnota X příslušnost k určité oblasti odpovídá jedné konkrétní hodnotu další proměnná y, Že y volal funkce proměnné x. Budeme psát symbolicky y=f(x). V tomto případě proměnná X volal nezávislé proměnné nebo argument.
Záznam y=C, Kde C– konstanta, označuje funkci, jejíž hodnota je libovolná X jeden a ten samý a rovný C.
Více významů X, pro které lze určit funkční hodnoty y podle pravidla f(x), volal doména funkce.
Všimněte si, že číselná posloupnost je také funkce, jejíž definiční obor se shoduje s množinou přirozená čísla.
Mezi základní elementární funkce patří všechny funkce studované v kurzu školní matematiky:
Elementární funkce je funkce, kterou lze specifikovat základními elementárními funkcemi a konstantami pomocí konečného počtu operací sčítání, odčítání, násobení, dělení a převzetí funkce.
KONCEPCE LIMITY ČÍSELNÉ SEKVENCE
V dalším kursu matematiky bude pojem limita hrát zásadní roli, protože základní pojmy s ní přímo souvisí. matematická analýza– derivace, integrál atd.
Začněme konceptem limity číselná řada.
Číslo A volal omezit sekvence X = {x n), jestliže pro libovolné předem určené libovolně malé kladné číslo ε takové přirozené číslo existuje Nže přede všemi n>N nerovnost |x n - a|< ε.
Pokud číslo A existuje limit sekvence X = {x n), pak to říkají x n usiluje o A, a piš.
Abychom tuto definici formulovali v geometrických pojmech, zavedeme následující pojem.
Okolí bodu x 0 se nazývá libovolný interval ( a, b), obsahující tento bod uvnitř sebe. Často se uvažuje o sousedství bodu x 0, pro který x 0 je tedy střed x 0 volal centrum sousedství a hodnota ( b–A)/2 – poloměr sousedství.
Pojďme tedy zjistit, co pojem limita číselné řady geometricky znamená. K tomu zapíšeme do formuláře poslední nerovnost z definice
Tato nerovnost znamená, že všechny prvky posloupnosti s čísly n>N musí ležet v intervalu (a – ε; a + ε).
Proto konstantní číslo A existuje omezení číselné řady ( x n), pokud pro jakoukoli malou čtvrť se středem v bodě A poloměr ε (ε je okolí bodu A) existuje takový prvek posloupnosti s číslem Nže všechny následující prvky jsou očíslovány n>N se bude nacházet v této blízkosti.
Příklady.
Udělejme několik poznámek.
Poznámka 1. Je zřejmé, že pokud všechny prvky číselné řady mají stejnou konstantní hodnotu x n = c, pak bude limita této posloupnosti rovna nejkonstantnější. Opravdu, pro jakékoli ε je nerovnost | x n - c| = |c - c| = 0 < ε.
Poznámka 2 Z definice limity vyplývá, že posloupnost nemůže mít dvě limity. Opravdu, dejme tomu x n → a a současně xn → b. Vezměte si libovolný a označte sousedství bodů A A b poloměr ε (viz obrázek). Pak podle definice limity musí být všechny prvky posloupnosti, počínaje určitým bodem, umístěny v blízkosti bodu A a v blízkosti bodu b, což je nemožné.
Poznámka 3. Neměli byste si myslet, že každá číselná řada má limit. Nechť například proměnná nabývá hodnot 
. Je snadné vidět, že tato sekvence nemá tendenci k žádnému limitu.
LIMIT FUNKCE
Nechte funkci y=f(x) definované v nějakém sousedství bodu A. Předpokládejme, že nezávislá proměnná X blíží se číslu bez omezení A. To znamená, že můžeme dávat X hodnoty co nejblíže A, ale ne rovné A. Označíme to takto x → a. Pro takové X Pojďme najít odpovídající hodnoty funkce. Může se stát, že hodnoty f(x) také přiblížit se k určitému počtu bez omezení b.Pak říkají, že číslo b existuje omezení funkce f(x) na x → a.
Zaveďme striktní definici limity funkce.
Funkce y=f(x) směřuje k limitě b jako x → a, jestliže pro každé kladné číslo ε, bez ohledu na to, jak je malé, lze zadat kladné číslo δ takové, že pro všechna x ≠ a z definičního oboru funkce splňující nerovnost | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b existuje omezení funkce f(x) na x → a, pak píšou popř f(x) → b na x → a.
Ilustrujme tuto definici grafem funkce. Protože z nerovnosti | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при X Î ( A - δ, A+ δ) odpovídající hodnoty funkce f(x) Î ( b - ε, b+ ε), pak, vezmeme-li libovolné ε > 0, můžeme vybrat číslo δ takové, že pro všechny body X, ležící v δ – okolí bodu A, odpovídající body grafu funkce musí ležet uvnitř pruhu šířky 2ε ohraničeného přímkami y = b– ε a y = b + ε.
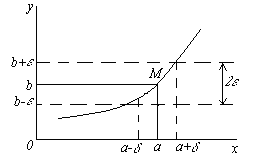
Je snadné vidět, že limita funkce musí mít stejné vlastnosti jako limita číselné posloupnosti, totiž x → a funkce má limitu, pak je jediná.
Příklady.
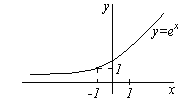
KONCEPCE LIMITU FUNKCE V NEKONEČNĚ VZDÁLENÉM BODĚ
Dosud jsme zvažovali limity pro případ, kdy proměnná X usiloval o určité konstantní číslo.
Řekneme, že proměnná x má sklon k nekonečnu, pokud pro každé předem určené kladné číslo M(může být libovolně velká) můžete zadat tuto hodnotu x=x 0, od kterého všechny následující hodnoty proměnné vyhoví nerovnosti |x|>M.
Nechte například proměnnou X nabývá hodnot X 1 = –1, X 2 = 2, X 3 = –3, …, X n = (–1) n n,… Je jasné, že se jedná o nekonečně velkou proměnnou, protože pro všechny M> 0 všechny hodnoty proměnné, počínaje určitou hodnotou, budou vyšší v absolutní hodnotě M.
Proměnná hodnota x → +∞, pokud pro svévolné M> 0 všechny následující hodnoty proměnné, počínaje určitou hodnotou, splňují nerovnost x > M.
Rovněž, X→ – ∞, pokud existuje M > 0 X< -M .
Řekneme, že funkce f(x) inklinuje k limitu b na X→ ∞, lze-li pro libovolné malé kladné číslo ε zadat takové kladné číslo M, což pro všechny hodnoty X, uspokojující nerovnost |x|>M, nerovnost | f(x) - b| < ε.
jmenovat .
Příklady.
NEKONEČNĚ VELKÉ VLASTNOSTI
Dříve jsme se podívali na případy, kdy funkce f(x) usiloval o nějakou konečnou hranici b na x → a nebo X → ∞.
Podívejme se nyní na případ, kdy funkce y=f(x) nějaký způsob, jak změnit argument.
Funkce f(x) inklinuje k nekonečnu jako x → a, tj. je nekonečně velký velikost, pokud pro jakékoli číslo M, bez ohledu na to, jak velký může být, je možné najít δ > 0 takové, že pro všechny hodnoty X≠A, splňující podmínku | x-a| < δ, имеет место неравенство |f(x)| > M.
Li f(x) inklinuje k nekonečnu jako x→a, pak píšou popř f(x)→∞ v x→a.
Formulujte podobnou definici pro případ, kdy X→∞.
Li f(x) inklinuje k nekonečnu jako x→a a zároveň přijímá pouze pozitivní nebo pouze záporné hodnoty, respektive napište nebo .
Příklady.
OMEZENÉ FUNKCE
Nechť je funkce dána y=f(x), definované na nějaké množině D hodnoty argumentů.
Funkce y=f(x) volal omezený na sadě D, pokud existuje kladné číslo M takové, že pro všechny hodnoty X z uvažovaného souboru nerovnost platí |f(x)|≤M. Pokud takové číslo M neexistuje, pak funkce f(x) volal neomezený na sadě D.
Příklady.
- Funkce y= hřích X, definované na -∞<X<+∞, является ограниченной, так как при всех значениях X|hřích X|≤1 = M.
- Funkce y=x 2 +2 je omezeno např. na segment, protože pro všechny X z tohoto segmentu |f(x)| ≤f(3) = 11.
- Zvažte funkci y=ln X na XО (0; 1). Tato funkce je v zadaném intervalu neomezená, od kdy X→0 log X→-∞.
Funkce y=f(x) volal ohraničené jako x → a, pokud existuje sousedství se středem v bodě A, ve kterém je funkce omezena.
Funkce y=f(x) volal ohraničené jako x→∞, pokud takové číslo existuje N> 0, což pro všechny hodnoty X |x|>N, funkce f(x) omezený.
Vytvořme spojení mezi omezenou funkcí a funkcí, která má limitu.
Věta 1. Li b je konečné číslo, pak funkce f(x) omezený kdy x→a.
Důkaz. Protože , pak pro libovolné ε>0 existuje číslo δ>0 takové, že pro všechny hodnoty X, uspokojující nerovnost |x-a|<
δ, nerovnost platí |f(x) –b|<
ε. Použití vlastnosti modulu |f(x) – b|≥|f(x)| - |b|, zapíšeme poslední nerovnost ve tvaru |f(x)|<|b|+
ε. Pokud tedy položíme M=|b|+ε, pak kdy x→a |f(x)|
Komentář. Z definice omezené funkce vyplývá, že jestliže , pak je neomezená. Opak však neplatí: ne omezená funkce nemusí být nekonečně velké. Uveďte příklad.
Věta 2. Pokud , pak funkce y=1/f(x) omezený kdy x→a.
Důkaz. Z podmínek věty vyplývá, že pro libovolné ε>0 v nějakém okolí bodu A my máme |f(x) – b|<
ε. Protože |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, Že |b| - |f(x)|<
ε. Proto, |f(x)|>|b| -ε >0. Proto 
OMEZIT. KONTINUITA FUNKCÍ
PROMĚNNÉ A KONSTANTY V důsledku měření fyzikálních veličin (čas, plocha, objem, hmotnost, rychlost atd.) jsou určeny jejich číselné hodnoty. Matematika se zabývá veličinami, abstrahuje od jejich konkrétního obsahu. V následujícím, když mluvíme o veličinách, budeme mít na mysli jejich číselné hodnoty. Při různých jevech se některé veličiny mění, jiné si zachovávají svou číselnou hodnotu. Například, když se bod pohybuje rovnoměrně, čas a vzdálenost se mění, ale rychlost zůstává konstantní. Proměnná hodnota je veličina, která nabývá různých číselných hodnot. Volá se veličina, jejíž číselné hodnoty se nemění konstantní. Variabilní množství budou označena písmeny x, y, z…, konstantní - a, b, c,… Všimněte si, že v matematice je konstantní hodnota často považována za zvláštní případ proměnné, ve které jsou všechny číselné hodnoty stejné. Změnit oblast Proměnná je množina všech číselných hodnot, které přijímá. Oblast změny se může skládat z jednoho nebo více intervalů nebo jednoho bodu. OBJEDNÁVANÉ VARIABILNÍ MNOŽSTVÍ. ČÍSELNÁ POŘADÍŘekneme, že proměnná X Tady je objednaná proměnná, pokud je známa oblast jeho změny a pro každou z jeho dvou hodnot lze říci, která z nich je předchozí a která je následující. Zvláštním případem objednané proměnné veličiny je proměnná veličina, jejíž hodnoty tvoří číselná řada X 1 ,X 2 ,…,X n ,… Pro takové hodnoty při i< j, i, j Î N , význam X i je považován za předchůdce a X j– následující bez ohledu na to, která z těchto hodnot je větší. Číselná posloupnost je tedy proměnná, jejíž po sobě jdoucí hodnoty lze přečíslovat. Číselnou posloupnost budeme označovat . Jednotlivá čísla v posloupnosti se nazývají jeho Prvky. Například číselná posloupnost je tvořena následujícími veličinami:
FUNKCE Při studiu různých přírodních jevů a řešení technických problémů a následně i v matematice je nutné uvažovat o změně jedné veličiny v závislosti na změně jiné. Například je známo, že plocha kruhu je vyjádřena jako poloměr vzorcem S = πr 2
. Pokud poloměr r nabývá různých číselných hodnot, pak plochy S nabývá také různých číselných hodnot, tzn. změna jedné proměnné způsobí změnu jiné. Pokud každá proměnná hodnota X příslušnost k určité oblasti odpovídá jedné konkrétní hodnotě jiné proměnné y, Že y volal funkce proměnné x. Budeme psát symbolicky y=f(x). V tomto případě proměnná X volal nezávislé proměnné nebo argument. Záznam y=C, Kde C– konstanta, označuje funkci, jejíž hodnota je libovolná X jeden a ten samý a rovný C. Více významů X, pro které lze určit funkční hodnoty y podle pravidla f(x), volal doména funkce. Všimněte si, že číselná posloupnost je také funkce, jejíž definiční obor se shoduje s množinou přirozených čísel. Mezi základní elementární funkce patří všechny funkce studované v kurzu školní matematiky: Elementární funkce je funkce, kterou lze specifikovat základními elementárními funkcemi a konstantami pomocí konečného počtu operací sčítání, odčítání, násobení, dělení a převzetí funkce. KONCEPCE LIMITY ČÍSELNÉ SEKVENCE V dalším kursu matematiky bude pojem limita hrát zásadní roli, protože s ní přímo souvisí základní pojmy matematické analýzy - derivace, integrál atd. Začněme pojmem limita číselné posloupnosti. Číslo A volal omezit sekvence X = {X n), jestliže pro libovolné předem určené libovolně malé kladné číslo ε takové přirozené číslo existuje Nže přede všemi n>N nerovnost |x n - a|< ε. Если число A existuje limit sekvence X = {X n), pak to říkají X n usiluje o A, a piš. Abychom tuto definici formulovali v geometrických pojmech, zavedeme následující pojem. Okolí bodu x 0
se nazývá libovolný interval ( a, b), obsahující tento bod uvnitř sebe. Často se uvažuje o sousedství bodu X 0
, pro který X 0
je tedy střed X 0
volal centrum sousedství a hodnota ( b–A)/2 – poloměr sousedství. Pojďme tedy zjistit, co pojem limita číselné řady geometricky znamená. K tomu zapíšeme do formuláře poslední nerovnost z definice Tato nerovnost znamená, že všechny prvky posloupnosti s čísly n>N musí ležet v intervalu (a – ε; a + ε). S 
tedy konstantní číslo A existuje omezení číselné řady ( X n), pokud pro jakoukoli malou čtvrť se středem v bodě A poloměr ε (ε je okolí bodu A) existuje takový prvek posloupnosti s číslem Nže všechny následující prvky jsou očíslovány n>N se bude nacházet v této blízkosti. Příklady.
- Nechte proměnnou X přebírá hodnoty postupně
, pak pro splnění vztahu |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве N jakékoli přirozené číslo, které vyhoví nerovnosti, dostaneme to, co potřebujeme. Vezmeme-li tedy například putování N= 6, pro všechny n>6 budeme mít 
. Vezměme libovolné ε > 0. Uvažujme . Pak, jestliže nebo, tzn. . Zvolíme tedy libovolné přirozené číslo, které nerovnosti vyhovuje. Udělejme několik poznámek. Poznámka 1. Je zřejmé, že pokud všechny prvky číselné řady mají stejnou konstantní hodnotu X n =c, pak bude limita této posloupnosti rovna nejkonstantnější. Opravdu, pro jakékoli ε je nerovnost | X n - c| = |c - c| = 0 < ε. Z 
Poznámka 2 Z definice limity vyplývá, že posloupnost nemůže mít dvě limity. Opravdu, dejme tomu X n →a a současně X n →b. Vezměte si libovolný a označte sousedství bodů A A b poloměr ε (viz obrázek). Pak podle definice limity musí být všechny prvky posloupnosti, počínaje určitým bodem, umístěny v blízkosti bodu A a v blízkosti bodu b, což je nemožné. Poznámka 3. Neměli byste si myslet, že každá číselná řada má limit. Nechť například proměnná nabývá hodnot 
. Je snadné vidět, že tato sekvence nemá tendenci k žádnému limitu. | LIMIT FUNKCE Nechte funkci y=f(x) definované v nějakém sousedství bodu A. Předpokládejme, že nezávislá proměnná X blíží se číslu bez omezení A. To znamená, že můžeme dávat X hodnoty co nejblíže A, ale ne rovné A. Označíme to takto x → a. Pro takové X Pojďme najít odpovídající hodnoty funkce. Může se stát, že hodnoty f(x) také přiblížit se k určitému počtu bez omezení b.Pak říkají, že číslo b existuje omezení funkce f(x) na x → a. Zaveďme striktní definici limity funkce. Funkce y=f(x) směřuje k limitě b jako x → a, jestliže pro každé kladné číslo ε, bez ohledu na to, jak je malé, lze zadat kladné číslo δ takové, že pro všechna x ≠ a z definičního oboru funkce | x-a| < δ, имеет место неравенство |f(x) - b| < ε. Если b existuje omezení funkce f(x) na x → a, pak píšou popř f(x) → b na x → a. Ilustrujme tuto definici grafem funkce. Protože z nerovnosti | x-a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при X Î ( A - δ, A+ δ) odpovídající hodnoty funkce f(x) Î ( b - ε, b+ ε), pak, vezmeme-li libovolné ε > 0, můžeme vybrat číslo δ takové, že pro všechny body X, ležící v δ – okolí bodu A, odpovídající body grafu funkce musí ležet uvnitř pruhu šířky 2ε ohraničeného přímkami y = b– ε a y = b+ ε. Je snadné vidět, že limita funkce musí mít stejné vlastnosti jako limita číselné posloupnosti, totiž x → a funkce má limitu, pak je jediná. Příklady. Pomocí grafu danou funkci, je snadné si toho všimnout. |
|
KONCEPCE LIMITU FUNKCE V NEKONEČNĚ VZDÁLENÉM BODĚ Dosud jsme zvažovali limity pro případ, kdy proměnná X usiloval o určité konstantní číslo. Řekneme, že proměnná x má sklon k nekonečnu, pokud pro každé předem určené kladné číslo M(může být libovolně velká) můžete zadat tuto hodnotu x=x 0
, od kterého všechny následující hodnoty proměnné vyhoví nerovnosti |x|>M. Nechte například proměnnou X nabývá hodnot X 1 = –1, X 2 =
2, X 3 = –3, …, X n = (–1) n n,... Je jasné, že se jedná o nekonečně velkou proměnnou, protože pro všechny M> 0 všechny hodnoty proměnné, počínaje určitou hodnotou, budou vyšší v absolutní hodnotě M. Proměnná hodnota x → +∞, pokud pro svévolné M> 0 všechny následující hodnoty proměnné, počínaje určitou hodnotou, splňují nerovnost x > M. Rovněž, X→ – ∞, pokud existuje M > 0 X< -M
. Řekneme, že funkce f(x) inklinuje k limitu b na X→ ∞, lze-li pro libovolné malé kladné číslo ε zadat takové kladné číslo M, což pro všechny hodnoty X, uspokojující nerovnost |x|>M, nerovnost | f(x) - b| < ε. Обозначают . Příklady. N 
Již nyní lze dokázat, že pro libovolné ε bude nerovnost splněna co nejdříve |x|>M a číslo M musí být určeno volbou ε. Zapsaná nerovnost je ekvivalentní následujícímu, který bude platit if |x|> 1/ε=M. To znamená, že (viz obrázek). NEKONEČNĚ VELKÉ VLASTNOSTI Dříve jsme se podívali na případy, kdy funkce f(x) usiloval o nějakou konečnou hranici b na x → a nebo X→ ∞. Podívejme se nyní na případ, kdy funkce y=f(x) nějaký způsob, jak změnit argument. Funkce f(x) inklinuje k nekonečnu jako x → a, tj. je nekonečně velký velikost, pokud pro jakékoli číslo M, bez ohledu na to, jak velký může být, je možné najít δ > 0 takové, že pro všechny hodnoty X≠A, splňující podmínku | x-a| < δ, имеет место неравенство |f(x)| > M. Li f(x) inklinuje k nekonečnu jako x→a, pak píšou popř f(x)→∞ v x→a. Formulujte podobnou definici pro případ, kdy X→∞. Li f(x) inklinuje k nekonečnu jako x→a a přitom nabývá pouze kladných nebo pouze záporných hodnot, podle toho píší nebo . Příklady. 
OMEZENÉ FUNKCE Nechť je funkce dána y=f(x), definované na nějaké množině D hodnoty argumentů. Funkce y=f(x) volal omezený na sadě D, pokud existuje kladné číslo M takové, že pro všechny hodnoty X z uvažovaného souboru nerovnost platí |f(x)|≤M. Pokud takové číslo M neexistuje, pak funkce f(x) volal neomezený na sadě D. Příklady.
- Funkce y= hřích X, definované na -∞<X<+∞, является ограниченной, так как при всех значениях X|hřích X|≤1 = M. Funkce y=x 2 +2 je omezeno např. na segment, protože pro všechny X z tohoto segmentu |f(x)| ≤f(3) = 11. Uvažujme funkci y=ln X na XО (0; 1). Tato funkce je v zadaném intervalu neomezená, od kdy X→0 log X→-∞.
. NEKONEČNĚ VELKÉ A NEKONEČNĚ MALÉ FUNKCE
NEKONEČNĚ MALÉ FUNKCE A JEJICH ZÁKLADNÍ VLASTNOSTI Funkce y=f(x) volal infinitezimální na x→a nebo kdy X→∞, jestliže nebo , tzn. infinitezimální funkce je funkce, jejíž limita v daném bodě je nula. P
příklady. 
Vytvořme následující důležitý vztah: Teorém. Pokud je funkce y=f(x) reprezentovatelné s x→a jako součet konstantního čísla b a nekonečně malá velikost α(x): f (x)=b+ α(x)Že . Naopak, pokud , pak f (x)=b+α(x), Kde sekera)– nekonečně malý při x→a. Důkaz. Uvažujme o základních vlastnostech infinitezimálních funkcí. Věta 1. Algebraický součet dvou, tří a obecně libovolného konečného počtu infinitezimálů je nekonečně malá funkce. Důkaz. Uveďme důkaz pro dva termíny. Nechat f(x)=α(x)+β(x), kde a . Musíme to dokázat pro libovolné malé ε >
0 nalezeno δ>
0, takže pro X, uspokojující nerovnost |x – a|<δ
, provedeno |f(x)|<
ε. Opravme tedy libovolné číslo ε >
0. Jelikož podle podmínek věty α(x) je infinitezimální funkce, pak existuje taková δ 1 >
0, což je |x – a|<
δ 1 máme |α(x)|<
ε /
2.
Stejně tak od β(x) je nekonečně malé, pak existuje takové δ 2 >
0, což je |x – a|<
δ 2 máme | β(x)|<
ε /
2.
Pojďme vzít δ=min(δ 1 ,
δ2 }
.Pak v blízkosti bodu A poloměr δ
každá z nerovností bude uspokojena |α(x)|<
ε /
2 a | β(x)|<
ε /
2.
Proto v této čtvrti bude |f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|<
ε /2 +
ε /2=
ε, tj. |f(x)|<
ε, což je to, co bylo potřeba dokázat. Věta 2. Součin infinitezimální funkce sekera) pro omezenou funkci f(x) na x→a(nebo kdy x→∞) je nekonečně malá funkce. Důkaz. Od funkce f(x) je omezená, pak je jich celá řada M takové, že pro všechny hodnoty X z nějakého sousedství bodu a|f(x)|≤M. Navíc od sekera) je nekonečně malá funkce at x→a, pak pro libovolné ε >
0 je okolí bodu A, ve kterém bude nerovnost platit |α(x)|<
ε /M. Pak v menší z těchto čtvrtí, které máme | αf|<
ε /M= ε. A to znamená, že af– nekonečně malý. Pro tuto příležitost x→∞ dokazování se provádí obdobně. Z osvědčené věty vyplývá: Důsledek 1. Pokud a pak. Důsledek 2. Li c= konst, tedy . Věta 3. Podíl infinitezimální funkce α(x) za funkci f(x), jehož limita je různá od nuly, je infinitezimální funkce. Důkaz. Nechat 
. Potom 1 /f(x) má omezenou funkci. Proto ten zlomek 
je součin infinitezimální funkce a funkce omezené, tzn. funkce je nekonečně malá. 1. Obecný kulturní a praktický význam paradigmatu kontinuity a diferenciálního a integrálního počtu
EsejPříloha 1 Prvky aplikace matematiky v socioekonomickém a sociomanažerském výzkumu a v moderní podnikové praxi - možná aplikační témata pro abstrakty,
- Dokument
Tato kapitola popisuje platná jména proměnných a funkcí Mathcadu, předdefinované proměnné a reprezentace čísel komplexní čísla stejně snadno jako s těmi skutečnými.
"Funkce a grafy"
EsejChtěl bych vědět více o tom, co je funkce a grafy funkcí. Od 7. třídy jsme se učili algebru podle programu A.G. Mordkovič. Věřím, že koncept funkční závislost je jedním z ústředních principů v matematice a prostupuje všemi jejími aplikacemi.
Krátký přehled a referenční příručka. Kniha je první přehledovou a referenční příručkou o virtuální fyzice svého druhu a je určena širokému okruhu čtenářů, kteří se zajímají o problémy vědy obecně a fyziky zvláště.
RezervovatKniha je první recenze a referenční příručka o virtuální fyzice svého druhu a je určena pro široký kruhčtenáři zajímající se o problémy vědy obecně a fyziky zvláště.
Program přijímacích zkoušek do magisterských programů ve směru 010200. 68 Matematika. Aplikovaná matematika "Matematická analýza"
ProgramLimit číselné řady. Základní vlastnosti: jednoznačnost limity; omezená konvergentní sekvence; konvergence podposloupnosti konvergentní posloupnosti.
Nechť x je uspořádaná proměnná (například číselná posloupnost).
Definice.
Konstantní čísloAse nazývá limita proměnné x, pokud je nějaké libovolně malé kladné číslo nevzali jsme to, můžete zadat hodnotu pro proměnnou x tak, že všechny následující hodnoty proměnné vyhoví nerovnosti X-A .
Symbolicky se to píše xa nebo limx=a (z latinského limes - limit).
Geometricky tato definice znamená, že bez ohledu na to, jaké malé - okolí bodu a vezmeme, všechny následující hodnoty x za určitým bodem budou ležet v tomto okolí.
Z nákresu je zřejmé, že nerovnost 
znamená, že vzdálenost od bodu x k a je menší než . A to je interiér čtvrti. Bod x zjevně také splňuje dvojitou nerovnost a- 
a tyto jsou ekvivalentní.
O 
definice: Pro číselnou řadu (x n ) je a limita if 
můžete zadat čísloN takové, že pro všechny 
U členů posloupnosti leží uvnitř všechny hodnoty x N , x N +1 a dále 
- sousedství je nutností.
Proměnná x, jejíž hodnoty tvoří číselnou posloupnost x 1,x 2,…,x n, se často zapisuje jako člen posloupnosti x=x n nebo (x n). Například (1/n). Jedná se o proměnnou veličinu nebo sekvenci se společným členem x n =1/n: 1,1/2,1/3…
Příklad: Nechť proměnná x nabývá sekvenční hodnoty: x 1 =2/1, x 2 =3/2, x 3 =4/3, …,x n =(n+1)/n,… tzn. tvoří číselnou řadu. Pojďme to dokázat 
.
Pojďme vzít 
.
. Jakmile se číslo stane 
, budeme to brát jako N. Pak bude nerovnost platit 
. Ale pak je vše prokázáno.
Věta 1: limit konstantní hodnoty je rovna této konstantě. Důkaz: Konstantní hodnota je speciální případ proměnné - všechny její hodnoty =c: x=c/ Ale pak limc=c.
Věta 2: Proměnná x nemůže mít dvě limity.
Důkaz:Řekněme limx=a a limx=b. Pak 
A 
po nějaké hodnotěx. Ale pak
Protože 
libovolně malá, pak je nerovnost možná pouze tehdy, když a = b
Poznámka: Proměnná nesmí mít limit: x=x n =(-1) n =-1,+1,-1,+1. Vzdálenost k libovolnému bodu a od jeho hodnot –1,+1 nemůže být menší než 1/2 
(-1) n nemá limitu.
Předpokládali jsme, že a je číslo. Ale proměnná x může mít také sklon k nekonečnu.
Definice: Proměnná x má tendenci k nekonečnu, jestliže for 
počínaje určitou hodnotou x váha, zbývající hodnoty uspokojují nerovnost 
. Variablex má tendenci 
, je-li za stejných podmínek nerovnost x>M a k - 
, je-li za stejných podmínek nerovnost x<-M.
Если переменная X
стремится к бесконечности, то её называют
nekonečně velký a piš 
Příklad: x=x n = n2. Pojďme vzít 
>0. n 2 >M musí být splněno. n> 
. Jakmile n vyhoví této nerovnosti, pak pro všechna x n =n 2 je nerovnost splněna. Takže n 2 
nebo spíše n 2 
.
§3. Funkční limit.
Budeme předpokládat, že argument x funkce y=f(x) má tendenci k x 0 nebo .
Uvažujme chování funkce y v těchto případech.
Definice.
Nechť je funkce y=f(x) definována v určitém okolí bodu x 0. Číslo A se nazývá limita funkce pro xx 0, jestliže pro libovolné , jakkoli malé, lze zadat číslo takové, že pro všechna xx 0 a splňující nerovnost x-x 0 je splněna nerovnost f (x)-A.
Je-li A limita funkce f(x), pak píšou 
orf(x)A při xx 0.
O 
Definici lze ilustrovat takto geometricky.
Jestliže A je limita f(x) pro xx 0, pak vezmeme-li jakékoli -okolí bodu A, můžeme vždy označit takové -okolí bodu x 0, že pro všechna x z tohoto -okolí hodnoty funkce f(x) jsou vzdálené od A ne dále než , tzn. bude spadat do zvoleného -okolí bodu A, nebo každopádně část grafu odpovídající bodům x z -okolí leží celá v pruhu o šířce 2.
Je vidět, že čím menší , tím menší by mělo být .
Definice.
Nechť argument x směřuje k bodu x 0, přičemž po celou dobu má hodnoty xx 0 xx 0 , pak číslo A 1 (A 2), ke kterému funkce f(x) směřuje, se nazývá limita funkce f(x) v bodě x 0 vpravo (vlevo) nebo pravotočivé (levotočivé).
Píše se: lim x x0+0 f(x)=A 1, (lim x x0-0 f(x)=A 2).
Lze dokázat, že pokud existuje limita lim x x0 f(x) = A, pak v tomto bodě existují obě jednostranné limity a jsou si rovny, A 1 = A 2 = A. Obrácení: Pokud existují jednostranné limity a jsou stejné, pak existuje obecná limita. Pokud alespoň jedna neexistuje nebo se nerovnají, pak limita funkce neexistuje.
Příklad.
Dokažte, že f(x)=3x-2 má limitu v x1 rovnou 1.
Jakékoli , х 3.
Jako můžete vzít jakákoli kladná čísla /3; 0</3.
Dokázali, že pro jakékoli stačí vzít /3 tak, že z 0х f(x)-1, ale to znamená, že lim X (3x-2)=1.
Definice.
H 
Číslo A se nazývá limita funkce y=f(x) pro x, jestliže pro libovolné (bez ohledu na to, jak malé) lze zadat kladné číslo P takové, že pro všechny hodnoty x splňující nerovnost xP nerovnost f(x)-A.
Napište lim x f(x)=A.
Geometricky to znamená, že pro libovolné se graf funkce pro xp a x-p nachází v pruhu o šířce 2.
Příklad.
f(x)=1/x pro x, f(x)0.
Bez ohledu na to, co 0 vezmeme, bude graf funkce pro xP a x-P umístěn v pruhu o šířce 2.
1/х, 1/х, x1/, Р=1/.
Podobně definováno 
f(x)=Ai a 
f(x)=A 2. V prvním případě musí být splněna nerovnost f(x)-A 1 pro xP, ve druhém případě f(x)-A 2 pro x-P (P0 .
Tak, 
1/x=0 a 
1/x=0. Jejich rovnost nám umožňuje uvažovat o obecné hranici 
1/x=0.
2 Limit proměnné hodnoty. Nekonečně malá a nekonečně velká množství, souvislost mezi nimi.
Limita proměnné v určitém bodě je číselně rovna tomuto bodu. limx(xàa) = a
Funkce se nazývá infinitesimální v bodě, kde xàa pokud yà0. limf(x)_(xàa) = 0
Říká se, že funkce je nekonečně velká v bodě, kde xàa pokud yà0. limf(x)_(xàa) =<><>
Vztah mezi množstvím:
Pokud je y=Ф(х) nekonečně malé, pak 1/ф(х) je nekonečně nemocné
3 Infinitezimály, jejich základní vlastnosti.
Součet konečného počtu nekonečně malých veličin je nekonečně malá veličina.
Součin konečné funkce a nekonečně malé veličiny je nekonečně malá veličina.
Funkce v bodě a má konečnou limitu právě tehdy, když f(x) = A + U(x), kde U(x) je nekonečně malá veličina Alternativně to lze zapsat jako f(x) – A à 0
Porovnání infinitezimálních funkcí:
Pokud poměrová hranice jedné b.m. do dalšího b.m. se rovná nule, pak b.m., která byla v čitateli bělejší vyššího řádu. Pokud je tato limita rovna nekonečnu, pak naopak.
A pokud je hranice jejich poměru rovna určitému číslu, pak tyto b.m. stejné pořadí.
Pokud je limit 1, pak tyto dva b.m. jsou ekvivalentní.
Teorém 1: součin infinitezimál je nekonečno vyššího řádu než každá z nich.
ODA . Funkce a(x) se nazývá b/m, pokud je její limita v tomto typu rovna 0. Z této definice vyplývá následující vlastnost funkcí b/m:
a) Algebraický součet a součin b/m funkcí jsou b/m funkce.
b) Součin funkce b/m a omezené funkce je funkce b/m, tzn. pokud a(x)®0 pro x®x0 a f(x) je definováno a omezeno ($ C:½j(x)½£C) => j(x)a(x)®0 pro x®x0
Aby bylo možné rozlišit vozidla podle jejich rychlosti blížící se 0, je zavedeno následující. pojem:
1) Pokud je poměr 2 b/m a(x)/b(x)®0 v x®x0, pak říkají, že b/m a má vyšší řád menší než b.
2) Jestliže a(x)/b(x)®A¹0 pro x®x0 (číslo A), pak a(x) a b(x) se nazývají b/m stejného řádu.
3) jestliže a(x)/b(x)®1, pak a(x) a b(x) jsou považovány za ekvivalentní b/m (a(x)~b(x)), pro x®x0.
4) Jestliže a(x)/b^n(x)®А¹0, pak a(x) se nazývá b/m n-tého řádu vzhledem k b(x).
Podobné definice pro případy: x®x0-, x®x0+, x®-¥, x®+¥ a x®¥.
4 Funkční limit. Základní věty o limitách.
Definice limita: nechť φ(x) je funkce definovaná na množině X a a je limitní bod této množiny. Volá se číslo A omezit funkce pro x à a právě tehdy, když pro libovolné e existuje okolí bodu a takové, že |ф(x) – a|< |е|
Jiným způsobem se to zapíše jako f(x) à A pro x à a
Věta 1: Jestliže každý člen algebraického součtu konečného počtu funkcí má limitu, protože x tíhne k a, pak je limita tohoto algebraického součtu v x stejná. k a existuje a rovná se stejnému algebraickému součtu limit členů.
Důkaz: funkci reprezentujeme jako součet její limity a infinitesimály, sčítáme funkce a infinitezimály. Ukazuje se, že součet funkcí se od součtu limit liší o nekonečně malé množství, což znamená, že toto je limita.
Následek: Funkce může mít pouze jeden limit na úrovni x. do a. Dokázáno protikladem. Ukazuje se, že rozdíl mezi původními funkcemi směřuje k rozdílu mezi jejich limitami, tedy nula směřuje k rozdílu mezi limitami, a protože limita konstantní funkce je rovna funkci samotné a je jedinečná, pak dostaneme, že rozdíl limity je roven 0, tedy limity jsou stejné.
Teorém 2: Pokud má každý z faktorů součinu konečného počtu funkcí limitu v x à a, pak je limita součinu v x a rovna součinu limit faktorů.
Důkaz: Uvažuje se součin dvou faktorů
Z různých způsobů, jak se proměnné chovají, je nejdůležitější ten, kdy proměnná tíhne k určité hranici. V tomto případě hodnoty nabyté proměnnou X, přiblížit se libovolně k nějakému konstantnímu číslu A- limit této proměnné. Říká se, že proměnná má tendenci se blížit konstantnímu číslu bez omezení. A(do svého limitu). Uveďme odpovídající definici podrobněji.
Proměnná x tíhne k limitě a (a - konstantní číslo), pokud je absolutní hodnota rozdíl mezi x a a se v procesu změny proměnné libovolně zmenšuje.
Stejnou definici lze říci jinými slovy.
Definice.Volá se konstanta avariabilní limitx pokud - absolutní hodnota rozdílu mezi x a a se v procesu změny proměnné x stane libovolně malou.
Skutečnost, že číslo A, je limit proměnné, zapsaný takto:
( - první písmena slova limes - limit) popř X->a
Ujasněme si, co je třeba chápat pod slovy „veličina se stává libovolně malou“ v definici limity. Nastavme libovolné kladné číslo , tedy if, počínaje od určitého okamžiku změny proměnné X, hodnoty budou a budou menší než toto 
.
Proměnná inklinuje k limitu jestliže pro nějaké kladné . od určitého okamžiku změny proměnné je nerovnost splněna 
.
Definice limity má jednoduchý geometrický význam: nerovnost znamená, že se nachází v -okolí bodu, tzn. v intervalu (obr. 26). Tedy definování limitu v geometrický tvar: číslo je limit proměnné, pokud je pro nějakou (libovolně malá)- sousedství bodu můžete určit okamžik změny proměnné, počínaje všemi jejími hodnotami
spadají do naznačeného sousedství bodu a.
Je třeba si představit proces přibližování se k limitu v dynamice. Vzal nějaké - sousedství bodu A; počínaje v určitém okamžiku změny , všechny hodnoty spadají do tohoto sousedství. Nyní se na to pojďme podívat blíž - sousedství bodu A; počínaje nějakým (ve srovnání s prvním) okamžikem změny , padnou všechny jeho hodnoty - sousedství bodu A atd. (Obr. 1).
 |
|||
 |
|||
Po zavedení definice limity proměnné hodnoty jsme se ji pokusili podrobně probrat a dešifrovat. V této definici však zůstal jeden velmi významný detail neodhalen; Co je třeba chápat pod slovy „počínaje určitým okamžikem změny proměnné“? To je jasné, když proces změny proměnné nastává v průběhu času: od určitého okamžiku (času). Ale ne vždy máme co do činění s proměnnými veličinami, k jejichž změně v čase dochází. Co dělat v těchto případech? Řešením je dešifrovat toto místo obecná definice omezte proměnnou specifickým způsobem pro každý typ proměnné: svým vlastním způsobem pro posloupnosti, svým vlastním způsobem pro funkce atd.
Limit konzistence. Nejprve si musíme zapamatovat definici posloupnosti: jsou-li všechny hodnoty převzaty proměnnou X, lze očíslovat pomocí všech možných přirozených čísel x), x 2,...x n,..., a hodnota s vyšším číslem se bere za hodnotu s nižším číslem, pak se říká, že proměnná je X prochází posloupností hodnot x x, x 2,... x n...; nebo jednoduše, že existuje posloupnost (číselná posloupnost).
Definice. Číselná posloupnost se nazývá reálná funkce přirozeného argumentu, tj. funkce, jejíž = N A EÌR.
Označuje se symbolem , kde nebo zkráceně . Číslo závislé na n se nazývá n – člen posloupnosti. Uspořádáme-li hodnoty sekvence v číselném pořadí, zjistíme, že sekvenci lze identifikovat pomocí spočítatelné sady reálná čísla, tj.
Příklady:
a) Posloupnost je konstantní a skládá se ze stejných čísel (jednotek): ;
b) 
. Pro ni
G) 
.
Pro posloupnosti platí tvrzení obsažené v obecné definici limity proměnné „od určitého okamžiku změny " musí znamenat "počínaje od určitého čísla", protože členy s vyššími čísly následují (podle definice posloupnosti) za členem s nižším číslem. Dostaneme tedy následující definici limity posloupnosti:
Definice. Číslo A volal omezit posloupnosti, pokud pro libovolné číslo existuje číslo takové, že všechna čísla, pro která splňují nerovnici.
Odpovídající označení
Nerovnici lze zapsat i ve tvaru 
nebo . Tyto záznamy zdůrazňují, že hodnota x n stane se co nejvíce k nerozeznání od A, kdy se počet členů neomezeně zvyšuje. Geometricky znamená definice limity posloupnosti následující: for libovolně malé -okolí čísla A existuje takové číslo N, že všechny členy posloupnosti jsou větší než N, čísla spadají do této blízkosti, Pouze konečný počet počátečních členů posloupnosti je mimo okolí (obr. 2). Jsou to všichni nebo někteří členové .
x 1 x 2 x N +1 a x N +2 x N x 3
Číslo v naší definici závisí na : N= N(). Jak již bylo zmíněno dříve, definici limitu je třeba chápat ve vývoji, v dynamice, v pohybu: vezmeme-li jinou, menší hodnotu pro , pak je obecně řečeno jiné číslo N x > N, taková ta nerovnost , je spokojený pro všechny .
Definici limity zapíšeme pomocí logických symbolů (kvantifikátorů). Definování limity posloupnosti pomocí kvantifikátorů vypadá takto.
