El algoritmo JPEG es un algoritmo de compresión de datos con pérdida. Algoritmos de archivo con pérdida
Las fotografías y las imágenes se diferencian entre sí no sólo en el contenido, sino también en otras características "informáticas". Por ejemplo, por tamaño.
Sucede que parecen haber dos dibujos idénticos, pero uno es tres veces más grande que el otro.
Las imágenes también difieren en calidad. Creo que más de una vez te has encontrado con fotografías de pésima calidad. Esto es visible a simple vista. Por ejemplo, dos fotografías idénticas, pero una es de mejor calidad y la otra de peor calidad.
Y sucede que al dibujo parece que le faltan colores. He aquí un ejemplo.

Y el formato o tipo de archivo es el responsable de todo esto.
De hecho, las imágenes vienen en una variedad de formatos. Y hay muchísimos de ellos. No los consideraremos todos, pero hablaremos de los más comunes. Se trata de formatos como bmp, gif, jpg, png, tiff.
Se diferencian entre sí, en primer lugar, en la calidad. Y la calidad difiere en la cantidad (saturación) de colores.
Por ejemplo, pinto un cuadro usando diferentes colores. Y de repente algunas se acaban y tienes que terminar de pintar con lo que tienes. Por supuesto, intentaré hacer todo lo posible para que esto no afecte mucho el resultado, pero aún así la imagen no saldrá como me gustaría: más descolorida, borrosa.
Así ocurre con los formatos de imagen. Algunos dejan todos los colores, mientras que otros cortan algunos. Y a veces esto hace que la imagen se deteriore.
Este es un ejemplo bastante aproximado. De hecho, todo es algo más complicado, pero creo que entendiste el punto principal.
Formatos de imagen comunes
BMP es un formato para dibujos realizados en el programa Paint. Se puede utilizar para almacenar imágenes dibujadas en su computadora. Pero este tipo de archivos no se utiliza en Internet debido a su gran tamaño. Entonces, si desea publicar una imagen dibujada en Paint en un blog o en una red social, debe ser de otro tipo: gif, jpg o png.
GIF es un formato de imagen popular en Internet. Puede guardarlos sin perder calidad, pero con un número limitado de colores: 256. GIF ha ganado especial popularidad debido a que puede crear pequeñas imágenes animadas (en movimiento).
JPG es un formato para fotografías y pinturas con una gran cantidad de colores. Puede guardar una imagen en él sin pérdida de calidad o con pérdida.
PNG es un formato de imagen moderno. Este tipo de imagen es de tamaño pequeño y sin pérdida de calidad. Muy cómodo: la lima es pequeña y la calidad es buena. También apoya la transparencia.
TIFF: las imágenes son de muy buena calidad, sin compresión, por lo que el tamaño de estos archivos es enorme. TIFF se utiliza cuando la calidad es de gran importancia. Por ejemplo, al crear tarjetas de visita, folletos, portadas de revistas.
Que formato elegir
- BMP: si se trata de un dibujo realizado en Paint y lo vas a conservar solo en la computadora.
- GIF: si es una animación o un dibujo con una pequeña cantidad de colores para su publicación en Internet.
- PNG: si se trata de una imagen que tiene muchos colores o algunas partes transparentes.
- JPG (jpeg): si es una fotografía.
- TIFF: imagen para impresión (tarjetas de visita, folletos, carteles, etc.).
Hola queridos amigos. Hoy hablaremos sobre qué formato de imagen es mejor usar en el sitio, qué formatos de archivos gráficos están disponibles para el sitio hoy y si es necesario buscar nuevos formatos gráficos.
Recibo muchas preguntas como esta; muchos de mis alumnos preguntan si pueden usar los nuevos formatos SVG y WebP y cuál es el mejor lugar para usar estas imágenes. Por supuesto, puedes utilizar nuevos formatos, sólo necesitas entender qué formato es más adecuado para qué.
Hoy en día, las imágenes en un sitio web son una parte integral. Desde el diseño gráfico hasta las imágenes de los artículos, los gráficos acompañan a la mayoría de los sitios en la web. Pero la belleza tiene un precio.
Las imágenes no optimizadas son uno de los factores que ralentizan un sitio web, tal y como indican los servicios de verificación.
Por tanto, siempre tendrás que decidir qué formato elegir para la imagen. De esto dependerá su tamaño y calidad. Y para utilizar imágenes más pequeñas sin perder calidad, necesitas saber algunas cosas.
¿Qué imágenes para sitios web uso hoy en día?
Todas las imágenes para sitios web se dividen en:
- ráster (ejemplo: JPG, JPEG, GIF, PNG),
- vector (ejemplo - SVG).
Ráster Las imágenes están formadas por píxeles que almacenan valores de color y transparencia. Estos formatos incluyen imágenes en artículos, botones, íconos y elementos de diseño. Estas imágenes son populares entre los desarrolladores y propietarios de sitios web. La principal desventaja de las imágenes rasterizadas es que no se escalan bien.
Es decir, cuando aumenta el tamaño de la imagen, se produce una pérdida de calidad.

Vector Las imágenes constan de líneas y puntos de referencia. La información de la imagen se almacena en instrucciones de representación matemática, lo que permite escalar dichas imágenes tanto como se desee sin pérdida de calidad.
Todas estas imágenes pueden utilizarse y se utilizan en sitios web modernos. ¡Solo necesita comprender eso antes de subir al sitio!
Descripción de formatos de imagen populares para el sitio.
A partir de la descripción de estos formatos, comprenderá dónde y qué formato se utiliza mejor en el sitio.
JPEG
JPEG o JPG es uno de los formatos de imagen más populares para sitios web. El formato admite millones de colores, lo que le otorga una posición de liderazgo en la presentación de fotografías e imágenes en el sitio.
Las imágenes en este formato están optimizadas bastante bien sin prácticamente ninguna pérdida de calidad, lo que le permite obtener un archivo más pequeño sin pérdida visual de calidad. Cabe recordar que cada optimización posterior reduce la calidad.
Los archivos de este formato son compatibles con todos los dispositivos y navegadores, lo que una vez más confirma su popularidad y le permite no preocuparse por los problemas de visualización en los sitios web.
La gran desventaja de este formato es la falta de transparencia. Es decir, no será posible combinar imágenes en este formato. Para tales tareas es mejor utilizar el siguiente formato.
PNG
Este formato utiliza un algoritmo de compresión sin pérdidas. En cuanto a número de colores y nivel de transparencia, está disponible en dos tipos: 8 y 24 bits. Ambos apoyan la transparencia.
Los 8 bits no son muy populares, pero los 24 bits se utilizan ampliamente para varias imágenes del sitio. Debido a la transparencia, le permite crear imágenes combinadas. A menudo se utiliza para crear botones e íconos animados donde se necesita un efecto de transparencia.
Las imágenes en formato PNG se pueden optimizar y editar muchas veces; conservarán la calidad original.
El formato también es compatible con todos los navegadores y dispositivos, lo que garantiza que se pueda mostrar en cualquier pantalla.
La calidad de las imágenes parece mejor que la de JPG, pero el peso del archivo será mayor. Esto debe tenerse en cuenta al colocar archivos en el sitio.
GIF
Es un formato de 8 bits que admite 256 colores, transparencia y animación. Debido a la compatibilidad con una pequeña cantidad de colores, el peso del archivo también es mínimo.
El formato no es adecuado para fotografías e imágenes con una amplia gama de colores.
Pero se usa ampliamente en la creación de pancartas, botones, íconos, etc.
En los sitios web modernos este formato se utiliza cada vez menos.
A continuación, hablemos de los formatos relativamente recientes SVG y WebP, que no son tan populares, pero están ganando popularidad y soporte, y se adaptan perfectamente a los requisitos de velocidad de carga y adaptabilidad del sitio web.
SVG
Es un formato de archivo vectorial basado en XML. El formato comenzó a ganar popularidad recientemente, ya que anteriormente no era compatible con los navegadores. Y debido a problemas de visualización, nadie tenía prisa por utilizarlo.
Hoy en día, SVG es compatible con todos los navegadores modernos. Pero todavía surgen problemas con la visualización.
Este formato se utiliza con mayor frecuencia para imágenes simples como logotipos, elementos de diseño, etc. No apto para fotografías.
El formato SVG es liviano, altamente escalable, proporciona imágenes nítidas en cualquier resolución de pantalla, admite animación, se puede controlar mediante CSS y colocar en HTML, lo que reduce la cantidad de solicitudes.
WebP
Un formato de código abierto desarrollado por Google específicamente para Internet. Hoy en día, YouTube utiliza la conversión de miniaturas de vídeos a WebP.

El formato proporciona una compresión superior y admite transparencia. Combina los beneficios de los formatos JPG y PNG sin aumentar el tamaño del archivo.
Pero, a pesar de las ventajas del formato, no es compatible con todos los navegadores, por ejemplo, IE, Edge, Firefox y Safari.
Hay formas de evitar estas restricciones, pero impiden que el formato se utilice en todas partes.
Conclusión
Amigos, espero haberles explicado todo claramente y ahora sepan qué formato de imagen es mejor usar en el sitio y por qué no insisto en usar un formato en particular, sino que recomiendo un enfoque integrado.
Quizás cuando WebP obtenga un soporte generalizado, todos cambiaremos a él y reemplazaremos jpg y png en nuestros sitios.
Analicemos en los comentarios qué formatos utiliza en sus sitios, qué le gusta y qué no le gusta.
Eso es todo por hoy, espero tus comentarios.
Saludos cordiales, Maxim Zaitsev.
- Color binario de 1 bit (21 = 2 colores), representado con mayor frecuencia por blanco y negro (o negro y verde)
- Color de 2 bits (22 = 4 colores) CGA, escala de grises NeXTstation
- Color de 3 bits (23 = 8 colores) muchas computadoras personales heredadas con salida de TV
- El color de 4 bits (24 = 16 colores) se conoce como EGA y, en menor medida, como estándar VGA de alta resolución.
- Color de 5 bits (25 = 32 colores) Conjunto de chips Amiga original
- Color de 6 bits (26 = 64 colores) Conjunto de chips Amiga original
- Color de 8 bits (28 = 256 colores) Estaciones de trabajo Unix heredadas, VGA de baja resolución, Super VGA, AGA
- Color de 12 bits (212 = 4096 colores) en algunos sistemas Silicon Graphics, sistemas NeXTstation y sistemas en modo Amiga HAM.
- Algoritmos de compresión sin pérdidas;
- Algoritmos de compresión con pérdida.
CON Los tres formatos de archivo más populares son JPEG, RAW y TIFF. A veces se pueden escuchar desacuerdos entre los fotógrafos: qué formato de archivo es mejor para la fotografía, en qué formato es mejor tomar fotografías, porque las cámaras modernas le permiten tomar fotografías.Fotografía en cualquiera de estos formatos y, a veces, en varios a la vez.
El formato de archivo en el que se almacena una imagen es esencialmente un compromiso entre la calidad de la imagen y el tamaño del archivo.
Probablemente ya sepas que una imagen rasterizada está formada por píxeles. La forma en que se organiza un archivo ráster y en qué forma se almacena la información sobre los píxeles determina el formato del archivo. La calidad de imagen de un archivo rasterizado está determinada por dos parámetros principales: el tamaño del píxel (es decir, el número total de píxeles) y la precisión del color del píxel al representar el color real.Con el tamaño de píxel está claro: cuantos más píxeles (o cuanto más “pequeño” sea el píxel), mejor.Y la precisión de la reproducción del color depende de la cantidad de colores por píxel o de la profundidad del color.
Profundidad de color (calidad de reproducción del color, profundidad de bits de la imagen): la cantidad de memoria en la cantidad de bits utilizados para almacenar y representar el color al codificar un píxel de gráficos rasterizados o una imagen de video. El número de bits indica el número de gradaciones (pasos de tono) en cada componente de color o, simplemente, el número de colores. Agregar 1 bit es agregar un bit más al código de color binario.



Por ejemplo, trabajamos en el espacio de color RGB. Esto significa que hay tres canales a partir de los cuales se forma el color final del píxel: el canal rojo (Rad), el canal verde (Green) y el canal azul (Blue). Supongamos que los canales son de cuatro bits. Esto significa que cada canal tiene la capacidad de mostrar 16 colores. Como resultado, todo el RGB será de 12 bits y podrá mostrar
C=16x16x16=4096 colores
La profundidad de color en este caso es de 12 bits.
Cuando la gente habla de RGB de 24 bits, se refiere a canales de 8 bits (256 colores cada uno) con un número total de opciones de color por píxel.
C=256x256x256=16777216 colores.
La cifra es impresionante. Esta cantidad de colores por cada píxel satisface los requisitos del fotógrafo más exigente.
Un poco sobre los formatos mismos.
formato TIFF
TIFF significa formato de archivo de imagen etiquetado y es un estándar para la industria de la impresión y la impresión.
Como resultado, esto es lo que sucede:
1. Si tu cámara es tan simple que solo graba JPEG y quieres la máxima calidad, configura el tamaño máximo y la compresión mínima y no te dejes atormentar por el hecho de que no tienes otros formatos. En la mayoría de los casos, una imagen RAW renderizada minuciosamente manualmente coincide con el JPEG capturado automáticamente por la cámara.
2. Probablemente no deberías tomar fotografías en TIFF. Grabar en este formato es más complicado, pero no hay una diferencia notable en comparación con JPEG de alta calidad.
3. Si tienes la oportunidad de tomar fotografías en , trabaja con ello. Sentirás por ti mismo si es adecuado para ti. En algunos casos, solo RAW permite tomar una fotografía única con gran aumento al imprimir.
Queda una solución más, se podría decir universal. Existe un modo que te permite tomar fotogramas en dos formatos simultáneamente: RAW+ JPEG. Graba escenas importantes en este modo. El almacenamiento de información digital moderno, tanto en tarjetas de memoria como en discos duros, lo permite. En este caso, recibirás un JPEG para utilizar la foto inmediatamente, sin perder tiempo en revisión. Y, si lo necesita, confíe el archivo RAW a un especialista para su procesamiento.
Foto. Formatos de archivo.
Es fácil calcular que una imagen a todo color sin comprimir con un tamaño de 2000 * 1000 píxeles tendrá un tamaño de aproximadamente 6 megabytes. Si hablamos de imágenes obtenidas con cámaras profesionales o escáneres de alta resolución, entonces su tamaño puede ser incluso mayor. A pesar del rápido crecimiento de la capacidad de los dispositivos de almacenamiento, varios algoritmos de compresión de imágenes siguen siendo muy relevantes.
Todos los algoritmos existentes se pueden dividir en dos grandes clases:
Algoritmos de compresión sin pérdidas
algoritmo RLE
Todos los algoritmos de la serie RLE se basan en una idea muy simple: los grupos repetidos de elementos se reemplazan por un par (número de repeticiones, elemento repetido). Consideremos este algoritmo usando el ejemplo de una secuencia de bits. Esta secuencia alternará grupos de ceros y unos. Además, los grupos suelen tener más de un elemento. Entonces la secuencia 11111 000000 11111111 00 corresponderá al siguiente conjunto de números 5 6 8 2. Estos números indican el número de repeticiones (el conteo comienza desde las unidades), pero estos números también deben codificarse. Supondremos que el número de repeticiones está en el rango de 0 a 7 (es decir, 3 bits son suficientes para codificar el número de repeticiones). Luego, la secuencia discutida anteriormente se codifica mediante la siguiente secuencia de números 5 6 7 0 1 2. Es fácil calcular que codificar la secuencia original requiere 21 bits, y en forma comprimida RLE esta secuencia toma 18 bits.Aunque este algoritmo es muy simple, su eficiencia es relativamente baja. Además, en algunos casos, el uso de este algoritmo no conduce a una disminución, sino a un aumento en la longitud de la secuencia. Por ejemplo, considere la siguiente secuencia 111 0000 11111111 00. La secuencia RL correspondiente se ve así: 3 4 7 0 1 2. La longitud de la secuencia original es de 17 bits, la longitud de la secuencia comprimida es de 18 bits.
Este algoritmo es más eficaz para imágenes en blanco y negro. También se suele utilizar como una de las etapas intermedias de compresión de algoritmos más complejos.
Algoritmos de diccionario
La idea detrás de los algoritmos de diccionario es que se codifican cadenas de elementos de la secuencia original. Esta codificación utiliza un diccionario especial, que se obtiene en función de la secuencia original.Existe toda una familia de algoritmos de diccionario, pero veremos el algoritmo más común, LZW, que lleva el nombre de sus desarrolladores Lepel, Ziv y Welch.
El diccionario de este algoritmo es una tabla que se llena con cadenas de codificación a medida que se ejecuta el algoritmo. Cuando se decodifica el código comprimido, el diccionario se restaura automáticamente, por lo que no es necesario transmitir el diccionario junto con el código comprimido.
El diccionario se inicializa con todas las cadenas singleton, es decir las primeras líneas del diccionario representan el alfabeto en el que codificamos. Durante la compresión, se busca la cadena más larga ya registrada en el diccionario. Cada vez que se encuentra una cadena que aún no se ha escrito en el diccionario, se agrega allí y se genera un código comprimido correspondiente a la cadena ya escrita en el diccionario. En teoría, no se imponen restricciones sobre el tamaño del diccionario, pero en la práctica tiene sentido limitar este tamaño, ya que con el tiempo comienzan a aparecer cadenas que ya no se encuentran en el texto. Además, cuando duplicamos el tamaño de la tabla, debemos asignar un bit extra para almacenar códigos comprimidos. Para evitar tales situaciones, se introduce un código especial que simboliza la inicialización de la tabla con todas las cadenas de un solo elemento.
Veamos un ejemplo de un algoritmo de compresión. Comprimiremos la línea cuckoocuckooocuckoohood. Supongamos que el diccionario contendrá 32 posiciones, lo que significa que cada uno de sus códigos ocupará 5 bits. Inicialmente, el diccionario se completa de la siguiente manera:
Esta tabla existe tanto del lado de quien comprime la información como del lado de quien la descomprime. Ahora veremos el proceso de compresión.

La tabla muestra el proceso de completar el diccionario. Es fácil calcular que el código comprimido resultante ocupa 105 bits y el texto original (suponiendo que gastemos 4 bits codificando un carácter) ocupa 116 bits.
De hecho, el proceso de decodificación se reduce a la decodificación directa de códigos, y es importante que la tabla se inicialice de la misma manera que durante la codificación. Ahora veamos el algoritmo de decodificación.

Podemos definir completamente la cadena agregada al diccionario en el i-ésimo paso solo en i+1. Obviamente, la línea i-ésima debe terminar con el primer carácter de la línea i+1. Eso. Acabamos de descubrir cómo restaurar un diccionario. De cierto interés es la situación cuando se codifica una secuencia de la forma cScSc, donde c es un carácter y S es una cadena, y la palabra cS ya está en el diccionario. A primera vista puede parecer que el decodificador no será capaz de solucionar esta situación, pero en realidad todas las líneas de este tipo deben terminar siempre con el mismo carácter con el que empiezan.
Algoritmos de codificación estadística.
Los algoritmos de esta serie asignan el código comprimido más corto a los elementos más frecuentes de las secuencias. Aquellos. Las secuencias de la misma longitud se codifican con códigos comprimidos de diferentes longitudes. Además, cuanto más a menudo ocurre una secuencia, más corto será el código comprimido correspondiente.Algoritmo de Huffman
El algoritmo de Huffman le permite construir códigos de prefijo. Podemos pensar en los códigos de prefijo como rutas en un árbol binario: ir de un nodo a su hijo izquierdo corresponde a un 0 en el código, y a su hijo derecho corresponde a un 1. Si etiquetamos las hojas del árbol con los símbolos Para codificarlo, obtenemos una representación de árbol binario del código de prefijo.Describamos el algoritmo para construir un árbol de Huffman y obtener códigos de Huffman.
- Los caracteres del alfabeto de entrada forman una lista de nodos libres. Cada hoja tiene un peso que es igual a la frecuencia de aparición del símbolo.
- Se seleccionan dos nodos de árbol libres con los pesos más pequeños.
- Su padre se crea con un peso igual a su peso total.
- El padre se agrega a la lista de nodos libres y sus dos hijos se eliminan de esta lista.
- A un arco que sale del padre se le asigna el bit 1, al otro se le asigna el bit 0
- Los pasos a partir del segundo se repiten hasta que solo quede un nodo libre en la lista de nodos libres. Esta será considerada la raíz del árbol.
Codificación aritmética
Los algoritmos de codificación aritmética codifican cadenas de elementos en una fracción. En este caso, se tiene en cuenta la distribución de frecuencia de los elementos. Por el momento, los algoritmos de codificación aritmética están protegidos por patentes, por lo que sólo veremos la idea básica.JPEG es uno de los algoritmos nuevos y bastante potentes. Es prácticamente el estándar de facto para imágenes a todo color. El algoritmo opera en áreas de 8x8 en las que el brillo y el color cambian con relativa suavidad. Como resultado, al descomponer una matriz de dicha área en una serie doble en cosenos (ver fórmulas a continuación), solo los primeros coeficientes son significativos. Por lo tanto, la compresión en JPEG se realiza debido a la suavidad de los cambios de color en la imagen.
El algoritmo fue desarrollado por un grupo de expertos en fotografía específicamente para comprimir imágenes de 24 bits. JPEG - Grupo Conjunto de Expertos en Fotografía - una división dentro de ISO - la Organización Internacional de Normalización. El nombre del algoritmo se lee como ["jei"peg]. En general, el algoritmo se basa en una transformada de coseno discreta (en lo sucesivo denominada DCT) aplicada a la matriz de imagen para obtener una nueva matriz de coeficientes. Se aplica una transformación inversa para obtener la imagen original.
DCT descompone la imagen según las amplitudes de determinadas frecuencias. Así, al transformar, obtenemos una matriz en la que muchos coeficientes son cercanos o iguales a cero. Además, debido a las imperfecciones de la visión humana, es posible aproximar los coeficientes de forma más aproximada sin una pérdida notable de calidad de la imagen.
Para ello se utiliza la cuantificación de coeficientes. En el caso más sencillo, se trata de un desplazamiento aritmético bit a bit hacia la derecha. Con esta conversión se pierde algo de información, pero se puede conseguir un mayor grado de compresión.
Cómo funciona el algoritmo
Entonces, veamos el algoritmo con más detalle (Fig. 2.1). Comprimamos una imagen de 24 bits.
Paso 1. Convertimos la imagen del espacio de color RGB, con componentes responsables de los componentes rojo, verde y azul del color puntual, al espacio de color YCrCb (a veces llamado YUV).
En él, Y es el componente de brillo y Cr, Co son los componentes responsables del color (rojo cromático y azul cromático). Debido a que el ojo humano es menos sensible al color que al brillo, es posible archivar matrices de componentes de Cr y Co con grandes pérdidas y, en consecuencia, altas relaciones de compresión. Una conversión similar se utiliza desde hace mucho tiempo en televisión. Allí se asigna una banda de frecuencia más estrecha para las señales responsables del color. Se puede representar una traducción simplificada del espacio de color RGB al espacio de color YCrCb mediante una matriz de transición:
Paso 2. Dividimos la imagen original en matrices de 8x8. Formamos 3 matrices DCT funcionales de cada una: 8 bits por separado para cada componente. En relaciones de compresión más altas, este paso puede resultar un poco más difícil. La imagen se divide por el componente Y, como en el primer caso, y para los componentes Cr y Cb las matrices se escriben a través de una fila y a través de una columna. Es decir, de la matriz original de 16x16, solo se obtiene una matriz DCT funcional. En este caso, como es fácil de ver, perdemos 3/4 de la información útil sobre los componentes de color de la imagen e inmediatamente recibimos una compresión doble. Podemos hacer esto trabajando en el espacio YCrCb. Como ha demostrado la práctica, esto no tiene un efecto significativo en la imagen RGB resultante.
Paso 3. En forma simplificada, DCT para n=8 se puede representar de la siguiente manera:
nu,v] = ^Hc(i,u)xC(j,v)y ry) y q= EnteroRedondo En este paso es donde se controla la relación de compresión y donde se producen las mayores pérdidas. Está claro que al especificar MK con coeficientes grandes, obtendremos más ceros y, por tanto, una mayor relación de compresión. Los efectos específicos del algoritmo también están asociados con la cuantificación. Con valores de gamma altos, la pérdida en bajas frecuencias puede ser tan grande que la imagen se divide en cuadrados de 8x8. Las pérdidas a altas frecuencias pueden manifestarse en los llamados efecto gibbs, cuando se forma una especie de “halo” alrededor de los contornos con una transición de color nítida. Paso 5. Convertimos la matriz de 8x8 en un vector de 64 elementos mediante escaneo en zig-zag, es decir, tomamos elementos con índices (0,0), (0,1), (1,0), (2,0). . Así, al principio del vector obtenemos coeficientes matriciales correspondientes a las bajas frecuencias y al final a las altas. Paso 6. Colapsamos el vector usando el algoritmo de codificación de grupo. En este caso obtenemos pares del tipo<пропустить, число>, donde "omitir" es el recuento de ceros omitidos y "número" es el valor que se colocará en la siguiente celda. Así, el vector 42 3000-2 00001 ... se plegará en pares (0,42) (0,3) (3,-2) (4,1).... Paso 7. Colapsamos los pares resultantes usando la codificación de Huffman con una tabla fija. El proceso de restauración de imágenes en este algoritmo es completamente simétrico. El método le permite comprimir algunas imágenes entre 10 y 15 veces sin pérdidas importantes. Los aspectos positivos importantes del algoritmo son que: ■ el nivel de compresión está establecido; ■ La imagen en color de salida puede tener 24 bits por punto. Los aspectos negativos del algoritmo son que: ■ A medida que aumenta el nivel de compresión, la imagen se divide en cuadrados individuales (8x8). Esto se debe al hecho de que se producen grandes pérdidas en las bajas frecuencias durante la cuantificación y resulta imposible restaurar los datos originales. ■ Aparece el efecto Gibbs: halos a lo largo de los límites de las transiciones de color nítidas. Como ya se mencionó, JPEG se estandarizó hace relativamente poco tiempo, en 1991. Pero incluso entonces había algoritmos que comprimían más fuertemente con menos pérdida de calidad. El hecho es que las acciones de los desarrolladores del estándar estaban limitadas por el poder de la tecnología que existía en ese momento. Es decir, incluso en una PC, el algoritmo tenía que ejecutarse durante menos de un minuto en una imagen promedio, y su implementación en hardware tenía que ser relativamente simple y barata. El algoritmo tenía que ser simétrico (el tiempo de descompresión es aproximadamente igual al tiempo de archivado). El cumplimiento de este último requisito hizo posible la aparición de dispositivos como las cámaras digitales que toman fotografías de 24 bits en una tarjeta flash de 8 a 256 MB." Luego, esta tarjeta se inserta en una ranura de su computadora portátil y el programa correspondiente le permite para leer las imágenes. Nya, si el algoritmo fuera asimétrico, sería desagradable esperar mucho tiempo hasta que el dispositivo se “recargue” y comprima la imagen. Otra propiedad no muy agradable de JPEG es Eso, que a menudo las rayas horizontales y verticales en la pantalla son completamente invisibles y solo pueden aparecer cuando se imprimen en forma de patrón muaré. Ocurre cuando se superpone una trama de impresión inclinada sobre las franjas horizontales y verticales de la imagen. Debido a estas sorpresas, JPEG no es recomendado activamente utilizado en impresión, estableciendo altos coeficientes de matriz de cuantificación. Sin embargo, actualmente resulta indispensable a la hora de archivar imágenes destinadas a la visualización humana. Ancho El uso de JPEG durante mucho tiempo estuvo limitado, quizás, solo por el hecho de que funciona con imágenes de 24 bits. Por lo tanto, para ver una imagen con una calidad aceptable en un monitor normal en una paleta de 256 colores, se requirió el uso de algoritmos adecuados y, en consecuencia, una cierta cantidad de tiempo. En aplicaciones destinadas a usuarios exigentes, como los juegos, estos retrasos son inaceptables. Además, si tiene imágenes, digamos, en formato GIF de 8 bits, convertidas a JPEG de 24 bits y luego de nuevo a GIF para verlas, la pérdida de calidad se producirá dos veces durante ambas conversiones. Sin embargo, el aumento en el tamaño del archivo suele ser tan grande (de 3 a 20 veces) y la pérdida de calidad es tan pequeña que almacenar imágenes en JPEG es muy eficaz. Es necesario decir algunas palabras sobre las modificaciones de este algoritmo. Aunque JPEG es un estándar ISO, su formato de archivo no se ha corregido. Aprovechando esto, los fabricantes crean sus propios formatos que son incompatibles entre sí y, por tanto, pueden cambiar el algoritmo. Así, las tablas de algoritmos internos recomendadas por ISO son sustituidas por las propias. Además, existe una ligera confusión a la hora de fijar el grado de pérdida. Por ejemplo, durante las pruebas resulta que la calidad "excelente", "100%" y "10 puntos" dan imágenes significativamente diferentes. Sin embargo, dicho sea de paso, una calidad “100%” no significa una compresión sin pérdidas. También hay opciones JPEG para aplicaciones específicas. Como estándar ISO, JPEG se utiliza cada vez más para intercambiar imágenes en redes informáticas. El algoritmo JPEG es compatible con los formatos Quick Time, PostScript Nivel 2, Tiff 6.0 y actualmente ocupa un lugar destacado en los sistemas multimedia. Características del algoritmo JPEG: o ! w. ,. Índice de compresión: 2-200 (establecido por el usuario). ,ts, :_,. . Clase de imagen: imágenes 2jj.bit a todo color o iso-| reflejos en escala de grises sin transiciones de color nítidas (fotos). Simetría: 1. Características:¡En algunos casos el algoritmo crea! "halo" alrededor de límites horizontales y verticales nítidos en una imagen (efecto Gibbs). Además, con una relación de compresión alta, iso-! La imagen está dividida en bloques de 8x8 píxeles. Conocer el algoritmo JPEG es muy útil no sólo para la compresión de imágenes. Utiliza teorías del procesamiento de señales digitales, análisis matemático, álgebra lineal, teoría de la información, en particular, transformada de Fourier, codificación sin pérdidas, etc. Por tanto, los conocimientos adquiridos pueden resultar útiles en cualquier lugar. Si lo desea, le sugiero que siga los mismos pasos usted mismo en paralelo con el artículo. Compruebe qué tan apropiado es el razonamiento anterior para diferentes imágenes, intente realizar sus propias modificaciones al algoritmo. Es muy interesante. Como herramienta, puedo recomendar la maravillosa combinación de Python + NumPy + Matplotlib + PIL(Pillow). Casi todo mi trabajo (incluidos gráficos y animaciones) se realizó usando ellos. ¡Atención, tráfico! Muchas ilustraciones, gráficos y animaciones (~ 10Mb). Irónicamente, en el artículo sobre JPEG sólo hay 2 imágenes con este formato entre cincuenta. Entrenaremos con gatos mapaches. La imagen gris de arriba se toma como ejemplo. Combina bien zonas homogéneas y contrastantes. Y si aprendemos a comprimir el gris, no habrá problemas con el color. Puedes pensar mentalmente en cómo se podría descomponer una señal cuyos valores disminuyen gradualmente desde un valor máximo al principio hasta un valor mínimo al final. Una aproximación más o menos adecuada sólo se puede lograr mediante los armónicos hacia el final, lo que para nosotros no es muy bueno. La figura de la izquierda es una aproximación de una señal de un solo extremo. A la derecha - simétrico: Entonces, se te ocurrió la idea de idear tu propia transformación. Recuerda esto: Los bloques grandes no se muestran, ya que visualmente son casi indistinguibles de los de 32x32. Ahora veamos la diferencia absoluta con la imagen original (ampliada 2 veces, de lo contrario nada es realmente visible): El 8x8 da mejores resultados que el 4x4. Un mayor aumento de tamaño ya no proporciona una ventaja claramente visible. Aunque consideraría seriamente 16x16 en lugar de 8x8: aumentar la complejidad en un 33% (más sobre la complejidad en el siguiente párrafo) proporciona una mejora pequeña pero aún visible para la misma cantidad de coeficientes. Sin embargo, la elección de 8x8 parece bastante razonable y puede ser la media dorada. JPEG se publicó en 1991. Creo que esa compresión era muy difícil para los procesadores de esa época. Segundo argumento. Una cosa a tener en cuenta es que aumentar el tamaño del bloque requerirá más cálculos. Calculemos cuánto. La complejidad de la conversión, como ya sabemos muy bien: O(N 2), ya que cada coeficiente consta de N términos. Pero en la práctica, se utiliza un algoritmo eficiente de Transformada Rápida de Fourier (FFT). Su descripción está fuera del alcance de este artículo. Su complejidad: O(N*logN). Para una expansión bidimensional necesitas usarla dos veces N veces. Entonces, la complejidad de 2D DCT es O (N 2 logN). Ahora comparemos la complejidad de calcular una imagen con un bloque y varios pequeños: Tercero argumento. Si tenemos un borde de colores nítido en la imagen, esto afectará a todo el bloque. Tal vez sería mejor que este bloque fuera lo suficientemente pequeño, porque en muchos bloques vecinos probablemente ya no existirá esa frontera. Sin embargo, lejos de los límites, la atenuación se produce con bastante rapidez. Además, la propia frontera se verá mejor. Comprobémoslo usando un ejemplo con una gran cantidad de transiciones de contraste, nuevamente con solo una cuarta parte de los coeficientes: Y de postre, considere un 5% de calidad (al codificar en Fast Stone). Por cierto, alrededor del 100% de calidad. Como se puede adivinar, en este caso la matriz de cuantificación consta enteramente de unidades, es decir, no se produce ninguna cuantificación. Sin embargo, debido al redondeo de los coeficientes al número entero más cercano, no podemos restaurar con precisión la imagen original. Por ejemplo, el mapache mantuvo exactamente el 96% de los píxeles, pero el 4% tenía un error de 1/256. Por supuesto, estas “distorsiones” no se pueden notar visualmente. Ejemplo 0(para calentar) Denotaremos palabras como A, B, C... y las llamaremos símbolos. Además, bajo el símbolo se puede esconder cualquier cosa: una letra del alfabeto, una palabra o un hipopótamo en el zoológico. Lo principal es que los símbolos idénticos corresponden a conceptos idénticos y los diferentes corresponden a otros diferentes. Dado que nuestra tarea es la codificación (compresión) eficiente, trabajaremos con bits, ya que son las unidades más pequeñas de representación de información. Por tanto, escribamos la lista como ABBAAABA. En lugar de "primera palabra" y "segunda palabra", se pueden utilizar los bits 0 y 1. Entonces ABBAAABA se codifica como 01100010 (8 bits = 1 byte). Ejemplo 1 Ejemplo 2 Ejemplo 3 Ejemplo 4 Ahora todo está en orden. Descubrimos cómo se almacenan los DC: Miremos AC: Construimos un histograma de la dependencia cuantitativa para estos pares y un árbol de Huffman. Características de implementación en JPEG: Descubrimos que cada bloque está codificado y almacenado en un archivo como este: Espero que ahora comprendas intuitivamente el algoritmo JPEG. ¡Gracias por leer! UPD Etiquetas: Agregar etiquetas Para comprimir datos de forma eficaz, primero debe evaluar la naturaleza de su imagen. JPEG comprime datos gráficos según lo que ve el ojo humano. Entonces, para ayudarlo a comprender cómo y qué hace JPEG, me gustaría brindarle una comprensión básica de la percepción visual humana. La compresión JPEG se produce en varias etapas. El objetivo es transformar datos gráficos para que la información visual irrelevante sea fácilmente identificada y descartada. Esta compresión "con pérdida" difiere de la mayoría de los otros enfoques utilizados con formatos gráficos, que intentan preservar intacto cada fragmento de la imagen. modelo de color El primer paso en JPEG es elegir una forma adecuada de representar los colores. Los colores suelen especificarse en un sistema de coordenadas tridimensional. Un sistema bien conocido por la mayoría de los programadores describe el color como una combinación de rojo, verde y azul (RGB). Desafortunadamente, desde el punto de vista de la compresión, esta no es la mejor manera de describir el color. El problema es que los tres componentes: rojo, verde y azul son equivalentes. Sin embargo, cambiar a un sistema de reproducción cromática diferente permite que se destaque información más importante. Los profesionales utilizan dos modelos de color: HSL (Hue-Saturation-Lightness) y HSV (Hue-Saturation-Value). Intuitivamente, el componente Luminosidad del modelo HSL y el Valor del modelo HSV definen cada uno la proporción de luz y sombra a su manera. La saturación determina el nivel de color "puro". Los colores insaturados a menudo se denominan informalmente "sucios" (grisáceos). El tono es lo que percibimos como el color de un objeto, como el rojo o el verde grisáceo. Aquí es importante señalar un hecho sorprendente: ¡la visión humana es más sensible a los cambios de luz y no al color como tal! Las diferentes implementaciones del algoritmo de compresión JPEG utilizan diferentes sistemas de color. El sistema de reproducción cromática YCbCr utilizado por el formato JFIF es en muchos aspectos similar al esquema desarrollado hace muchos años para la televisión en color. adelgazamiento La razón principal para convertir un modelo de color a otro es identificar información que es menos relevante para ver en una imagen. JPEG reduce la cantidad de información de color. Mientras que el componente luma se transmite a máxima resolución, los componentes de crominancia utilizan la mitad del rango de valores. Este sencillo paso reduce el volumen de datos en un tercio. Mediante el submuestreo, se ajustan los colores de una imagen de televisión en color. Normalmente, en la televisión, las imágenes en blanco y negro y la información en color se transmiten por separado. Además, la información sobre el color se transmite de forma menos estricta que la información sobre el brillo de la imagen. Transformada de coseno discreta (DCT) Cada componente de color se procesa por separado, como si no fueran una imagen en color, sino tres imágenes en escala de grises. Si miras una imagen detallada desde lejos, sólo discernirás el tono general de la imagen. Por ejemplo, "principalmente azul" o "principalmente rojo". Cuanto más te acerques a la imagen, más detalles podrás discernir. Para emular este efecto, JPEG utiliza una técnica matemática llamada transformada de coseno discreto (DCT). DCT convierte la información de píxeles en información de cambio de píxeles. Lo primero que puede proporcionar DCT es el color medio del área. Luego elabora más y más detalles. Como en el caso de una imagen lejana, el valor de color promedio representa información muy importante sobre el área de la imagen. Su ojo es menos sensible a la velocidad del cambio de color, por lo que no es tan importante. Al transformar la información del color de esta manera, resaltamos la información que se puede sacrificar. Se cree que esta etapa provoca pérdidas. Si codifica una imagen con DCT y luego utiliza la función DCT inversa para reconstruirla, no obtendrá exactamente el mismo conjunto de bits. Sin embargo, este error es un error de redondeo. Ocurre al realizar operaciones aritméticas y no suele ser muy grande. Por lo tanto, prefiero pensar en la etapa DCT como una actividad "mayormente sin pérdidas". Para imágenes grandes, calcular DCT y DCT inversa es un proceso que requiere mucho tiempo. Para reducir el tiempo de cálculo, JPEG divide la imagen en un mosaico de ocho por ocho píxeles. Cada mosaico se procesa por separado, lo que reduce significativamente el tiempo de cálculo requerido para DCT. El problema con este enfoque es que después de la cuantificación (que se discutirá en la siguiente sección), los límites de estos cuadrados pueden no coincidir y, por lo tanto, volverse visibles cuando el parámetro de calidad se establece en un valor bajo. Cuantización Los desarrolladores de JPEG estaban interesados principalmente en imágenes de calidad fotográfica (fotográficas, de tono continuo). Normalmente, estas imágenes de medios tonos se caracterizan por suaves transiciones de un color a otro. Para tales imágenes, el componente de baja frecuencia (que cambia lentamente) del DCT es más importante que el componente de alta frecuencia (que cambia rápidamente). El término cuantificación significa simplemente "redondeo". JPEG descarta cierta información gráfica redondeando cada término DCT con diferentes pesos en función de diferentes factores. El componente de alta frecuencia está más redondeado que el componente de baja frecuencia. Por ejemplo, el componente de baja frecuencia que almacena el valor de brillo promedio puede redondearse a un múltiplo de tres, mientras que el componente de alta frecuencia puede redondearse a un múltiplo de cien. La operación de cuantización explica por qué la compresión JPEG produce líneas temblorosas cuando los bordes son nítidos. Los contornos están determinados por un componente espacial de alta frecuencia (que cambia rápidamente). (A primera vista, podría pensar que debería terminar con un contorno borroso, pero recuerde que la C en DCT significa coseno). Normalmente, los planos de color se cuantifican de forma mucho más basta que los planos de brillo. Aquí, la elección correcta del modelo de color ayuda a identificar información que puede descartarse. Compresión Hasta ahora, excepto cuando se considera la frecuencia de muestreo de dos canales de color, no se ha producido ninguna compresión. Todos los pasos discutidos anteriormente (conversión del modelo de color, DCT y cuantificación) dejaron el tamaño de los datos sin cambios. Finalmente llegamos al paso final, donde las técnicas estándar de compresión sin pérdidas realmente reducirán el tamaño de los datos. Los datos descompuestos en los pasos anteriores se pueden comprimir de manera más eficiente que la materia prima que son los datos de gráficos RGB. Además, ninguna de las medidas tomadas fue superflua; cada cambio en los datos tenía como objetivo comprimir de manera más efectiva la versión final. El cambio del modelo de color permitió diluir la información de los canales y luego cuantificarlos con mayor energía. DCT hizo posible aislar el componente espacial de alta frecuencia. El componente de alta frecuencia generalmente tiene valores pequeños, lo que hace que la salida de la etapa DCT contenga una cantidad desproporcionada de valores pequeños para facilitar el proceso de compresión. Durante el proceso de cuantización, la mayor parte del componente de alta frecuencia se restablece a cero y el resto adquiere valores específicos. Reducir la cantidad de valores diferentes también facilita el proceso de compresión de datos. El estándar JPEG proporciona dos métodos diferentes de compresión sin pérdidas que se pueden utilizar como paso final. La compresión Huffman es un algoritmo fácilmente programable, no patentado y conocido desde hace mucho tiempo. Por el contrario, el algoritmo de codificación aritmética más nuevo es objeto de numerosas patentes (por lo que no es sorprendente que muchos programas de compresión JPEG solo admitan la compresión Huffman). Al decodificar imágenes JPEG, debes realizar todos estos pasos en orden inverso. Primero se descomprime el flujo de datos, luego cada 8-8 bloques se somete a DCT inversa y, finalmente, la imagen se convierte al modelo de color apropiado (generalmente RGB). Tenga en cuenta que la información que se ha descartado deliberadamente mediante diezmación y cuantificación nunca se recupera. Sin embargo, si todo se hizo correctamente, la pérdida de información no provocará ninguna degradación visible de la imagen. El algoritmo para convertir una imagen gráfica JPEG consta de varias etapas que se realizan en la imagen de forma secuencial, una tras otra: – conversiones de espacio de color, – submuestreo, – transformada de coseno discreta (DCT), – cuantificación, – codificación. En la etapa de conversión del espacio de color, la imagen se convierte del espacio de color RGB a YCbCr (donde Y es el brillo y Cb y Cr son los componentes de diferencia de color del punto de la imagen): Aplicación del espacio YCbCr en lugar de lo habitual RGB se explica por las características fisiológicas de la visión humana, es decir, el hecho de que el sistema nervioso humano tiene una sensibilidad significativamente mayor a la luminosidad ( Y) que a los componentes de diferencia de color (en este caso cb Y cr). Conversión inversa del espacio de color (de YCrCb V RGB) tiene la forma: El algoritmo de compresión JPEG le permite comprimir imágenes con diferentes tamaños de planos de color. Denotemos por xyo Y y yo anchura y altura iº plano de color de la imagen. Dejar X= máximo(xyo), Y= máximo(y yo), definimos para cada plano los coeficientes Hola= X/ xyo Y vi yo= Y/ y yo. El valor más alto para X Y Y según el algoritmo JPEG es 2 16, y para Hola Y vi yo– 2 2 . Por tanto, el ancho y la altura de los planos de color pueden ser de 1 a 4 veces más pequeños que las dimensiones del plano más grande. Para ordinario RGB imágenes, los tamaños de todos los planos de color son iguales. El submuestreo consiste en reducir el tamaño de los planos. cr Y cb. La reducción más común es 2 veces en ancho y 2 veces en altura (ver Figura 1). Para esto cr Y cb Los planos de la imagen se dividen en bloques de 2 por 2 píxeles y el bloque se reemplaza por una muestra de componentes de diferencia de color (en lugar de las 4 muestras existentes, se coloca su media aritmética para cada bloque, lo que hace que posible reducir el tamaño de la imagen original 2 veces). Figura 1 – Tipos comunes de reducción de resolución Luego, por separado para cada componente del espacio de color. Y, cb Y cr, se realiza una transformada de coseno discreta directa. Para ello, la imagen se divide en bloques de 8 por 8 píxeles y cada bloque se transforma según la fórmula: El uso de la transformación de coseno discreto le permite pasar de la representación espacial de la imagen a la espectral. La transformada inversa del coseno discreto tiene la forma: Después de esto, puede proceder a la cuantificación de la información recibida. La idea de la cuantificación es descartar una determinada cantidad de información. Se sabe que el ojo humano es menos sensible a las altas frecuencias (especialmente a las altas frecuencias de los componentes de diferencia de color). La mayoría de las imágenes fotográficas contienen pocos componentes de alta frecuencia; Además, la aparición de altas frecuencias es consecuencia del proceso de digitalización, es decir. debido a la aparición del ruido de muestreo y cuantificación que lo acompaña. En esta etapa, el llamado tablas de cuantificación- matrices que constan de números enteros positivos de 8 por 8, cuyos elementos se dividen en las frecuencias correspondientes de los bloques de imágenes, el resultado se redondea a un número entero: El proceso de descuantización utiliza las mismas tablas que la cuantificación. La descuantización consiste en multiplicar las frecuencias cuantificadas por los elementos correspondientes de la tabla de cuantificación: Así, a medida que aumenta el factor de cuantificación, aumenta la cantidad de información descartada. Veamos esto con más detalle usando un ejemplo. Bloque antes de la cuantización: 3862, –22, –162, –111, –414, 12, 717, 490, 383, 902, 913, 234, –555, 18, –189, 236, 229, 707, –708, 775, 423, –411, –66, –685, 231, 34, –928, 34, –1221, 647, 98, –824, –394, 128, –307, 757, 10, –21, 431, 427, 324, –874, –367, –103, –308, 74, –1017, 1502, 208, –90, 114, –363, 478, 330, 52, 558, 577, 1094, 62, 19, –810, –157, –979, –98 Tabla de cuantificación (calidad 90): 24, 16, 16, 24, 40, 64, 80, 96, 16, 16, 24, 32, 40, 96, 96, 88, 24, 24, 24, 40, 64, 88, 112, 88, 24, 24, 32, 48, 80, 136, 128, 96, 32, 32, 56, 88, 112, 176, 168, 120, 40, 56, 88, 104, 128, 168, 184, 144, 80, 104, 128, 136, 168, 192, 192, 160, 112, 144, 152, 160, 176, 160, 168, 160 Bloque después de la cuantificación: 161, –1, –10, –5, –10, 0, 9, 5, 24, 56, 38, 7, –14, 0, –2, 3, 10, 29, –30, 19, 7, –5, –1, –8, 10, 1, –29, 1, –15, 5, 1, –9, –12, 4, –5, 9, 0, 0, 3, 4, 8, –16, –4, –1, –2, 0, –6, 10, 3, –1, 1, –3, 3, 2, 0, 3, 5, 8, 0, 0, –5, –1, –6, –1 3864, –16, –160, –120, –400, 0, 720, 480, 384, 896, 912, 224, –560, 0, –192, 264, 240, 696, –720, 760, 448, –440, –112, –704, 240, 24, –928, 48,–1200, 680, 128, –864, –384, 128, –280, 792, 0, 0, 504, 480, 320, –896, –352, –104, –256, 0,–1104, 1440, 240, –104, 128, –408, 504, 384, 0, 480, 560, 1152, 0, 0, –880, –160,–1008, –160 Tabla de cuantificación (calidad 45): 144, 96, 88, 144, 216, 352, 456, 544, 104, 104, 128, 168, 232, 512, 536, 488, 128, 112, 144, 216, 352, 504, 616, 496, 128, 152, 192, 256, 456, 776, 712, 552, 160, 192, 328, 496, 600, 968, 912, 680, 216, 312, 488, 568, 720, 920, 1000, 816, 432, 568, 696, 776, 912, 1072, 1064, 896, 640, 816, 840, 872, 992, 888, 912, 880 Bloque después de la cuantificación: 27, 0, –2, –1, –2, 0, 2, 1, 4, 9, 7, 1, –2, 0, 0, 0, 2, 6, –5, 4, 1, –1, 0, –1, 2, 0, –5, 0, –3, 1, 0, –1, –2, 1, –1, 2, 0, 0, 0, 1, 2, –3, –1, 0, 0, 0, –1, 2, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, –1, 0, –1, 0 Bloquear después de la conversión inversa: 3888, 0, –176, –144, –432, 0, 912, 544, 416, 936, 896, 168, –464, 0, 0, 0, 256, 672, –720, 864, 352, –504, 0, –496, 256, 0, –960, 0,–1368, 776, 0, –552, –320, 192, –328, 992, 0, 0, 0, 680, 432, –936, –488, 0, 0, 0,–1000, 1632, 0, 0, 0, 0, 912, 0, 0, 896, 640, 816, 0, 0, –992, 0, –912, 0 Como se puede observar, en el primer caso el cambio corriente continua El coeficiente como resultado de la compresión es 2, y en el segundo 26, mientras está cuantificado. corriente continua el coeficiente en el segundo caso es 6 veces menor que en el primero. La codificación es la etapa final de la compresión; durante ella, los bloques de imágenes se convierten en forma vectorial de acuerdo con la regla especificada por bloques de la forma: 0, 1, 5, 6, 14, 15, 27, 28, 2, 4, 7, 13, 16, 26, 29, 42, 3, 8, 12, 17, 25, 30, 41, 43, 9, 11, 18, 24, 31, 40, 44, 53, 10, 19, 23, 32, 39, 45, 52, 54, 20, 22, 33, 38, 46, 51, 55, 60, 21, 34, 37, 47, 50, 56, 59, 61, 35, 36, 48, 49, 57, 58, 62, 63 donde los índices vectoriales de los componentes matriciales correspondientes se indican como elementos de bloque. En este caso, el elemento cero se codifica como la diferencia con el elemento cero del bloque anterior. Los elementos cero indican corriente continua, contienen el componente constante del bloque (todos los demás elementos de CA generalmente se indican C.A.). Luego, los datos resultantes se comprimen mediante codificación aritmética o una modificación del algoritmo de Huffman. Esta etapa no es de gran interés desde el punto de vista de la esteganografía en imágenes gráficas, por lo que escapa al alcance de nuestra consideración.
Por el título entendiste correctamente que esta no es una descripción muy común del algoritmo JPEG (describí el formato de archivo en detalle en el artículo "Decodificación de JPEG para principiantes"). En primer lugar, el método elegido para presentar el material supone que no sabemos nada no sólo sobre JPEG, sino también sobre la transformada de Fourier y la codificación de Huffman. En general, recordamos poco de las conferencias. Simplemente tomaron la fotografía y comenzaron a pensar en cómo podría comprimirse. Por lo tanto, traté de expresar claramente solo la esencia, pero en la que el lector desarrollará una comprensión bastante profunda y, lo más importante, intuitiva del algoritmo. Fórmulas y cálculos matemáticos: como mínimo, sólo aquellos que son importantes para comprender lo que está sucediendo.
Cualquiera que sea el algoritmo de compresión de información, su principio siempre será el mismo: encontrar y describir patrones. Cuantos más patrones, más redundancia, menos información. Los archivadores y codificadores suelen estar "adaptados" a un tipo específico de información y saben dónde encontrarla. En algunos casos, un patrón es inmediatamente visible, como una imagen de un cielo azul. Cada fila de su representación digital se puede describir con bastante precisión mediante una línea recta.Representación vectorial
Primero, comprobemos qué tan dependientes son dos píxeles vecinos. Es lógico suponer que lo más probable es que sean muy similares. Comprobemos esto para todos los pares de imágenes. Marquémoslos en el plano de coordenadas con puntos de modo que el valor del punto a lo largo del eje X sea el valor del primer píxel y a lo largo del eje Y, el segundo. Para nuestra imagen que mide 256 por 256, obtenemos 256*256/2 píxeles: 
Como era de esperar, la mayoría de los puntos están ubicados en o cerca de la línea y=x (y hay incluso más de los que se pueden ver en la figura, ya que se superponen entre sí muchas veces y, además, son translúcidos). De ser así, sería más fácil trabajar girándolos 45°. Para hacer esto, necesitas expresarlos en un sistema de coordenadas diferente. 
Los vectores básicos del nuevo sistema son obviamente: . Nos vemos obligados a dividir por la raíz de dos para obtener un sistema ortonormal (las longitudes de los vectores base son iguales a uno). Aquí se muestra que cierto punto p = (x, y) en el nuevo sistema se representará como un punto (a 0, a 1). Conociendo los nuevos coeficientes, podemos obtener fácilmente los antiguos dándoles la vuelta. Obviamente, la primera (nueva) coordenada es el promedio y la segunda es la diferencia de xey (pero dividida por la raíz de 2). Imagina que te piden que dejes solo uno de los valores: un 0 o un 1 (es decir, equiparar el otro a cero). Es mejor elegir un 0, ya que lo más probable es que el valor de un 1 sea cercano a cero. Esto es lo que pasa si restauramos la imagen solo desde un 0: 
Aumento 4x: 
Para ser honesto, esta compresión no es muy impresionante. Es mejor dividir la imagen de manera similar en tripletes de píxeles y presentarlos en un espacio tridimensional. 

Este es el mismo gráfico, pero desde diferentes puntos de vista. Las líneas rojas son los ejes que se sugirieron. Corresponden a los vectores: . Déjame recordarte que debes dividir por algunas constantes para que las longitudes de los vectores sean iguales a uno. Así, ampliando sobre esta base, obtenemos 3 valores un 0, un 1, un 2, y un 0 es más importante que un 1, y un 1 es más importante que un 2. Si descartamos un 2, entonces la gráfica se “aplanará” en la dirección del vector e 2. Esta lámina tridimensional, que ya es bastante delgada, se volverá plana. No perderá tanto, pero nos desharemos de un tercio de los valores. Comparemos imágenes reconstruidas a partir de tripletas: (a 0, 0, 0), (a 1, a 2, 0) y (a 0, a 1, a 2). En la última versión no tiramos nada, así que nos quedaremos con el original. 
Aumento 4x: 
El segundo dibujo ya está bueno. Las áreas nítidas se suavizaron un poco, pero en general la imagen se conservó muy bien. Y ahora, dividamos por cuatro de la misma manera y determinemos visualmente la base en el espacio de cuatro dimensiones... Oh, bueno, sí. Pero puedes adivinar cuál será uno de los vectores base: (1,1,1,1)/2. Por lo tanto, se puede observar la proyección del espacio de cuatro dimensiones sobre el espacio perpendicular al vector (1,1,1,1) para identificar otros. Pero esta no es la mejor manera.
Nuestro objetivo es aprender a transformar (x 0 , x 1 , ..., x n-1 ) en (a 0 , a 1 , ..., an-1 ) para que cada valor de a i sea menos importante que los anteriores. Si podemos hacer esto, entonces quizás los últimos valores de la secuencia puedan descartarse por completo. Los experimentos anteriores insinúan que es posible. Pero no se puede prescindir de un aparato matemático.
Por lo tanto, necesitamos transformar los puntos a una nueva base. Pero primero hay que encontrar una base adecuada. Volvamos al primer experimento de emparejamiento. Considerémoslo en general. Hemos definido los vectores base: 
Expresamos el vector a través de ellos. pag:
o en coordenadas: 
Para encontrar un 0 y un 1 necesitas proyectar pag en mi 0 y mi 1 respectivamente. Y para ello necesitas encontrar el producto escalar.
similar:
En coordenadas: 
A menudo es más conveniente realizar la transformación en forma matricial. 
Entonces A = EX y X = E T A. Esta es una forma hermosa y conveniente. La matriz E se llama matriz de transformación y es ortogonal, la veremos más adelante. Transición de vectores a funciones.
Es conveniente trabajar con vectores de pequeñas dimensiones. Sin embargo, queremos encontrar patrones en bloques más grandes, por lo que en lugar de vectores N-dimensionales es más conveniente operar con las secuencias que representan la imagen. Llamaré a estas secuencias funciones discretas, ya que el siguiente razonamiento también se aplica a funciones continuas.
Volviendo a nuestro ejemplo, imagine una función f(i), que está definida sólo en dos puntos: f(0)=x y f(1)=y. De manera similar, definimos las funciones base e 0 (i) y e 1 (i) con base en las bases mi 0 y mi 1 . Obtenemos: 
Ésta es una conclusión muy importante. Ahora, en la frase “expansión de un vector en vectores ortonormales” podemos reemplazar la palabra “vector” por “función” y obtener la expresión completamente correcta “expansión de una función en funciones ortonormales”. No importa que obtuviéramos una función tan corta, ya que el mismo razonamiento funciona para un vector N-dimensional, que se puede representar como una función discreta con N valores. Y trabajar con funciones es más claro que con vectores de N dimensiones. Por el contrario, puedes representar dicha función como un vector. Además, una función continua ordinaria puede representarse mediante un vector de dimensión infinita, aunque no en el espacio euclidiano, sino en el espacio de Hilbert. Pero no iremos allí; sólo nos interesarán las funciones discretas.
Y nuestro problema de encontrar una base se convierte en el problema de encontrar un sistema adecuado de funciones ortonormales. En el siguiente razonamiento, se supone que de alguna manera ya hemos determinado un conjunto de funciones básicas, según las cuales descompondremos.
Digamos que tenemos alguna función (representada, por ejemplo, por valores) que queremos representar como una suma de otras. Puedes representar este proceso en forma vectorial. Para descomponer una función, es necesario "proyectarla" en las funciones base una por una. En el sentido vectorial, calcular la proyección da la aproximación mínima del vector original a otro en términos de distancia. Recordando que la distancia se calcula utilizando el teorema de Pitágoras, una representación similar en forma de funciones proporciona la mejor aproximación cuadrática media de una función a otra. Así, cada coeficiente (k) determina la “cercanía” de la función. Más formalmente, k*e(x) es la mejor aproximación cuadrática media a f(x) entre l*e(x).
El siguiente ejemplo muestra el proceso de aproximar una función usando solo dos puntos. A la derecha hay una representación vectorial. 
En relación con nuestro experimento de división en pares, podemos decir que estos dos puntos (0 y 1 a lo largo de la abscisa) son un par de píxeles vecinos (x, y).
Lo mismo, pero con animación: 
Si tomamos 3 puntos, entonces debemos considerar vectores tridimensionales, pero la aproximación será más precisa. Y para una función discreta con N valores, es necesario considerar vectores N-dimensionales.
Teniendo un conjunto de coeficientes obtenidos, puede obtener fácilmente la función original sumando las funciones base tomadas con los coeficientes correspondientes. El análisis de estos coeficientes puede proporcionar mucha información útil (según la base). Un caso especial de estas consideraciones es el principio de expansión en series de Fourier. Después de todo, nuestro razonamiento es aplicable a cualquier base, y al expandirse a una serie de Fourier, se toma una completamente específica. Transformadas discretas de Fourier (DFT)
En la parte anterior llegamos a la conclusión de que sería bueno descomponer una función en sus componentes. A principios del siglo XIX, Fourier también pensó en esto. Es cierto que no tenía la imagen de un mapache, por lo que tuvo que estudiar la distribución del calor a lo largo del anillo de metal. Luego descubrió que es muy conveniente expresar la temperatura (y su cambio) en cada punto del anillo como una suma de sinusoides con diferentes períodos. "Fourier descubrió (recomiendo leer, es interesante) que el segundo armónico decae 4 veces más rápido que el primero, y los armónicos de orden superior decaen a un ritmo aún más rápido".
En general, pronto resultó que las funciones periódicas se pueden descomponer perfectamente en la suma de sinusoides. Y dado que en la naturaleza existen muchos objetos y procesos descritos mediante funciones periódicas, ha aparecido una poderosa herramienta para su análisis.
Quizás uno de los procesos periódicos más visuales sea el sonido. 
Si me hubieran dado los valores de la última función en ese momento en el que no sabía nada de las series de Fourier, y me hubieran pedido que los analizara, entonces definitivamente me habría confundido y no habría podido decir nada que valiera la pena. Bueno, sí, algún tipo de función, pero ¿cómo se entiende que hay algo ordenado ahí? Pero si hubiera adivinado escuchar la última función, mi oído habría captado un tono puro entre el ruido. Aunque no es muy bueno, ya que durante la generación seleccioné especialmente dichos parámetros para que en el gráfico resumen la señal se disolviera visualmente en ruido. Según tengo entendido, todavía no está claro exactamente cómo hace esto un audífono. Sin embargo, recientemente quedó claro que no descompone el sonido en ondas sinusoidales. Quizás algún día comprendamos cómo sucede esto y aparezcan algoritmos más avanzados. Bueno, por ahora lo estamos haciendo a la antigua usanza.
¿Por qué no intentar utilizar las sinusoides como base? De hecho, ya lo hemos hecho. Recordemos nuestra descomposición en 3 vectores básicos y presentémoslos en el gráfico: 
Sí, sí, lo sé, parece un ajuste, pero con tres vectores es difícil esperar más. Pero ahora está claro cómo obtener, por ejemplo, 8 vectores básicos: 
Una comprobación no muy complicada muestra que estos vectores son perpendiculares por pares, es decir, ortogonales. Esto significa que se pueden utilizar como base. La transformación sobre esta base es ampliamente conocida y se denomina transformada discreta del coseno (DCT). Creo que en los gráficos anteriores queda claro cómo se obtiene la fórmula de transformación DCT:
Sigue siendo la misma fórmula: A = EX con base sustituida. Los vectores base de la DCT especificada (también son vectores fila de la matriz E) son ortogonales, pero no ortonormales. Esto debe recordarse durante la transformación inversa (no me detendré en esto, pero para aquellos interesados, la DCT inversa tiene un término 0.5*a 0 , ya que el vector de base cero es mayor que los demás).
El siguiente ejemplo muestra el proceso de aproximar subtotales a los valores originales. En cada iteración, la siguiente base se multiplica por el siguiente coeficiente y se suma a la suma intermedia (es decir, lo mismo que en los primeros experimentos con el mapache: un tercio de los valores, dos tercios). 
Pero, sin embargo, a pesar de algunos argumentos sobre la conveniencia de elegir tal base, todavía no existen argumentos reales. De hecho, a diferencia del sonido, la viabilidad de descomponer una imagen en funciones periódicas es mucho menos obvia. Sin embargo, la imagen puede resultar demasiado impredecible incluso en un área pequeña. Por lo tanto, la imagen se divide en partes lo suficientemente pequeñas, pero no absolutamente pequeñas, para que la descomposición tenga sentido. En JPEG, la imagen se "corta" en cuadrados de 8x8. Dentro de una pieza de este tipo, las fotografías suelen ser muy uniformes: el fondo más pequeñas fluctuaciones. Las sinusoides se acercan maravillosamente a estas áreas.
Bueno, digamos que este hecho es más o menos intuitivo. Pero las transiciones de color repentinas tienen un mal presentimiento, porque cambiar lentamente las funciones no nos salvará. A esto hay que añadir varias funciones de alta frecuencia que cumplen su función, pero que aparecen de lado sobre un fondo homogéneo. Tomemos una imagen de 256x256 con dos áreas contrastantes: 
Ampliemos cada fila usando DCT, obteniendo así 256 coeficientes por fila.
Luego dejamos solo los primeros n coeficientes y ponemos el resto a cero y, por lo tanto, la imagen se presentará como una suma solo de los primeros armónicos: 
El número en la imagen es el número de probabilidades que quedan. En la primera imagen sólo queda el valor medio. En el segundo ya se ha añadido una sinusoide de baja frecuencia, etc. Por cierto, preste atención al borde: a pesar de la mejor aproximación, al lado de la diagonal se ven claramente 2 franjas, una más clara y la otra más oscura. Parte de la última imagen ampliada 4 veces:
Y, en general, si lejos del límite vemos un fondo uniforme inicial, cuando nos acercamos a él, la amplitud comienza a crecer, finalmente alcanza un valor mínimo y luego, de repente, se vuelve máximo. Este fenómeno se conoce como efecto Gibbs. 
La altura de estas jorobas, que aparecen cerca de las discontinuidades de la función, no disminuirá a medida que aumente el número de sumandos de las funciones. En una transformación discreta, desaparece sólo cuando se conservan casi todos los coeficientes. Más precisamente, se vuelve invisible.
El siguiente ejemplo es completamente similar a la descomposición de triángulos anterior, pero en un mapache real: 
Al estudiar la DCT, uno puede tener la falsa impresión de que sólo los primeros coeficientes (de baja frecuencia) siempre son suficientes. Esto es cierto para muchas fotografías, aquellas cuyos significados no cambian dramáticamente. Sin embargo, en el borde de áreas contrastantes los valores “saltarán” rápidamente e incluso los últimos coeficientes serán grandes. Por lo tanto, cuando escuche acerca de la propiedad de conservación de energía de la DCT, tenga en cuenta el hecho de que se aplica a muchos tipos de señales encontradas, pero no a todas. Por ejemplo, piense en cómo sería una función discreta cuyos coeficientes de expansión sean iguales a cero, excepto el último. Sugerencia: piense en la descomposición en forma vectorial.
A pesar de las deficiencias, la base elegida es una de las mejores en fotografías reales. Veremos una pequeña comparación con otros un poco más adelante. DCT frente a todo lo demás
Cuando estudié el tema de las transformaciones ortogonales, para ser honesto, no me convencieron mucho los argumentos de que todo lo que nos rodea es la suma de oscilaciones armónicas, por lo que es necesario descomponer las imágenes en sinusoides. ¿O tal vez algunas funciones escalonadas serían mejores? Por lo tanto, busqué resultados de investigaciones sobre la optimización de DCT en imágenes reales. El hecho de que “es la DCT la que se encuentra con mayor frecuencia en aplicaciones prácticas debido a la propiedad de “compactación de energía”” está escrito en todas partes. Esta propiedad significa que la cantidad máxima de información está contenida en los primeros coeficientes. ¿Y por qué? No es difícil realizar una investigación: nos armamos con un montón de imágenes diferentes, diferentes bases conocidas y comenzamos a calcular la desviación estándar de la imagen real para un número diferente de coeficientes. Encontré un pequeño estudio en un artículo (imágenes utilizadas) sobre esta técnica. Muestra gráficas de la dependencia de la energía almacenada del número de primeros coeficientes de expansión para diferentes bases. Si mirabas las listas, estabas convencido de que DCT ocupa constantemente un honorable... um... 3er lugar. ¿Cómo es eso? ¿Qué tipo de conversión KLT es esta? Estaba elogiando a DCT, y luego... KLT
Todas las transformaciones, excepto KLT, son transformaciones con base constante. Y en KLT (transformada de Karhunen-Loeve) se calcula la base más óptima para varios vectores. Se calcula de tal manera que los primeros coeficientes den el error cuadrático medio más pequeño en total para todos los vectores. Anteriormente realizamos un trabajo similar manualmente, determinando visualmente la base. Al principio parece una buena idea. Podríamos, por ejemplo, dividir la imagen en pequeñas secciones y calcular su propia base para cada una. Pero no sólo existe la preocupación de almacenar esta base, sino que además la operación de calcularla requiere bastante mano de obra. Pero DCT pierde sólo un poco y, además, DCT tiene algoritmos de conversión rápidos. DFT
DFT (Transformada de Fourier discreta): transformada de Fourier discreta. Bajo este nombre a veces se hace referencia no sólo a una transformación concreta, sino también a toda la clase de transformaciones discretas (DCT, DST...). Veamos la fórmula DFT: 
Como puedes imaginar, se trata de una transformación ortogonal con algún tipo de base compleja. Dado que una forma tan compleja ocurre con un poco más de frecuencia de lo habitual, tiene sentido estudiar su derivación.
Puede parecer que cualquier señal armónica pura (con una frecuencia entera) con descomposición DCT dará solo un coeficiente distinto de cero correspondiente a este armónico. Esto no es cierto, porque además de la frecuencia, también es importante la fase de esta señal. Por ejemplo, la expansión del seno en cosenos (de manera similar en la expansión discreta) será así:
Hasta aquí los armónicos puros. Ella engendró a muchos otros. La animación muestra los coeficientes DCT de una onda sinusoidal en diferentes fases. 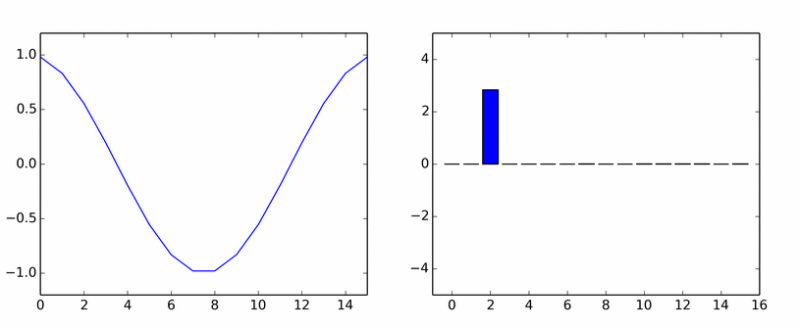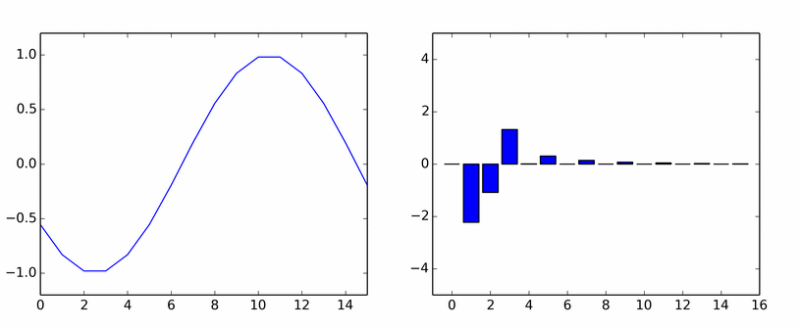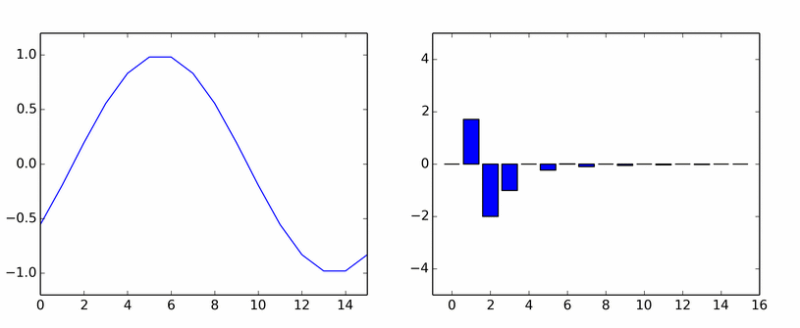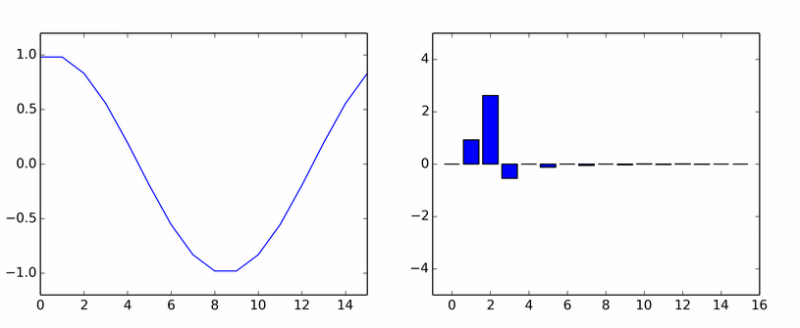
Si te parecía que las columnas giraban alrededor de un eje, entonces no te parecía.
Esto significa que ahora expandiremos la función a la suma de sinusoides no solo de diferentes frecuencias, sino también de aquellas desplazadas a lo largo de alguna fase. Será más conveniente considerar el cambio de fase usando el ejemplo del coseno:
Una identidad trigonométrica simple da un resultado importante: el desplazamiento de fase se reemplaza por la suma de seno y coseno, tomada con los coeficientes cos(b) y sin(b). Esto significa que las funciones se pueden expandir a la suma de senos y cosenos (sin fases). Esta es una forma trigonométrica común. Sin embargo, el complejo se utiliza con mucha más frecuencia. Para obtenerlo es necesario utilizar la fórmula de Euler. Simplemente sustituyendo las fórmulas derivadas del seno y el coseno, obtenemos: 
Ahora un pequeño cambio. El guión bajo es el número conjugado.
Obtenemos la igualdad final:
c es un coeficiente complejo, cuya parte real es igual al coeficiente del coseno y la parte imaginaria es igual al coeficiente del seno. Y el conjunto de puntos (cos(b), sin(b)) es un círculo. En una grabación de este tipo, cada armónico entra en la expansión con una frecuencia tanto positiva como negativa. Por lo tanto, en varias fórmulas de análisis de Fourier, la suma o integración suele ocurrir desde menos hasta más infinito. A menudo resulta más cómodo realizar cálculos en esta forma compleja.
La transformación descompone la señal en armónicos con frecuencias de una a N oscilaciones en la región de la señal. Pero la frecuencia de muestreo es N por área de señal. Y según el teorema de Kotelnikov (también conocido como teorema de Nyquist-Shannon), la frecuencia de muestreo debe ser al menos el doble de la frecuencia de la señal. Si este no es el caso, entonces el efecto es la aparición de una señal con una frecuencia falsa: 
La línea de puntos muestra la señal reconstruida incorrectamente. A menudo te has encontrado con este fenómeno en la vida. Por ejemplo, el divertido movimiento de las ruedas de un coche en un vídeo o el efecto muaré.
Esto lleva al hecho de que la segunda mitad de las N amplitudes complejas parece consistir en otras frecuencias. Estos falsos armónicos de la segunda mitad son un reflejo de la primera y no contienen información adicional. Por lo tanto, nos quedan N/2 cosenos y N/2 senos (formando una base ortogonal).
Vale, hay una base. Sus componentes son armónicos con un número entero de oscilaciones en la región de la señal, lo que significa que los valores extremos de los armónicos son iguales. Más precisamente, son casi iguales, ya que el último valor no se toma completamente del borde. Además, cada armónico es casi simétrico en relación con su centro. Todos estos fenómenos son especialmente fuertes en las bajas frecuencias, que son importantes para nosotros a la hora de codificar. Esto también es malo porque los límites de los bloques serán visibles en la imagen comprimida. Permítanme ilustrar la base DFT con N=8. Las primeras 2 filas son componentes cosenos, las últimas son senos: 
Preste atención a la aparición de componentes duplicados a medida que aumenta la frecuencia. 
Las cosas van extremadamente mal con el primero.
Entonces, ¿tal vez podamos hacerlo como en DCT: reducir las frecuencias en 2 u otro número de veces, de modo que el número de algunas oscilaciones sea fraccionario y los límites estén en diferentes fases? Entonces los componentes serán no ortogonales. Y no hay nada que hacer al respecto.horario de verano
¿Qué pasa si usamos senos en lugar de cosenos en DCT? Obtendremos la Transformada Sinusoidal Discreta (DST). Pero para nuestra tarea, todos ellos carecen de interés, ya que tanto el período completo como el semiperíodo de los senos están cerca de cero en los límites. Es decir, obtendremos aproximadamente la misma descomposición inapropiada que la de DFT. Regresando a DCT
¿Cómo le va en las fronteras? Bien. Hay antífases y no ceros. Todo el resto
Transformadas que no son de Fourier. No lo describiré.
WHT: la matriz consta únicamente de componentes escalonados con valores -1 y 1.
Haar es también una transformada wavelet ortogonal.
Son inferiores a DCT, pero más fáciles de calcular.
No será fácil, ¿verdad? Sin embargo, para algunos tipos de imágenes es posible seleccionar una base mejor que la de DCT. transformaciones 2D
Ahora intentemos realizar tal experimento. Tomemos, por ejemplo, un fragmento de una imagen. 
Su gráfico 3D: 
Repasemos DCT(N=32) a través de cada línea: 
Ahora quiero que repases con la vista cada columna de los coeficientes resultantes, es decir, de arriba a abajo. Recuerda que nuestro objetivo es dejar el menor número de valores posible, eliminando aquellos que no sean significativos. Probablemente hayas adivinado que los valores de cada columna de los coeficientes resultantes se pueden expandir exactamente de la misma manera que los valores de la imagen original. Nadie nos limita a la hora de elegir una matriz de transformación ortogonal, pero lo haremos nuevamente usando DCT(N=8): 
El coeficiente (0,0) resultó ser demasiado grande, por lo que se reduce 4 veces en el gráfico.
¿Entonces qué pasó?
La esquina superior izquierda son los coeficientes más significativos de la expansión de los coeficientes más significativos.
La esquina inferior izquierda son los coeficientes más insignificantes de la expansión de los coeficientes más significativos.
La esquina superior derecha son los coeficientes de expansión más significativos de los coeficientes más insignificantes.
La esquina inferior derecha son los coeficientes más insignificantes de la expansión de los coeficientes más insignificantes.
Está claro que la importancia de los coeficientes disminuye si se mueve en diagonal desde la parte superior izquierda a la inferior derecha. ¿Qué es más importante: (0, 7) o (7, 0)? ¿Qué quieren decir?
Primero, por filas: A 0 = (EX T) T = XET (transpuesto, ya que la fórmula es A=EX para columnas), luego por columnas: A=EA 0 = EXE T . Si calculas cuidadosamente, obtienes la fórmula:
Por lo tanto, si un vector se descompone en sinusoides, entonces la matriz se descompone en funciones de la forma cos(ax)*cos(by). Cada bloque de 8x8 en JPEG se representa como una suma de 64 funciones de la forma: 
En Wikipedia y otras fuentes, estas funciones se presentan en una forma más conveniente: 
Por tanto, los coeficientes (0, 7) o (7, 0) son igualmente útiles.
Sin embargo, en realidad se trata de una descomposición unidimensional ordinaria en 64 bases de 64 dimensiones. Todo lo anterior se aplica no sólo a DCT, sino también a cualquier descomposición ortogonal. Procediendo por analogía, en el caso general obtenemos una transformación ortogonal de N dimensiones.
Y aquí hay una transformación 2D de un mapache (DCT 256x256). De nuevo con los valores puestos a cero. Números: el número de coeficientes distintos de cero de todos (se conservaron los valores más significativos, ubicados en el área triangular en la esquina superior izquierda). 
Recuerda que el coeficiente (0, 0) se llama DC, los 63 restantes se llaman AC. Elegir un tamaño de bloque
Un amigo pregunta por qué JPEG usa particiones de 8x8. De la respuesta rechazada: El DCT trata el bloque como si fuera periódico y tiene que reconstruir el salto resultante en los límites. Si toma bloques de 64x64, lo más probable es que tenga un gran salto en los límites y necesitará muchos componentes de alta frecuencia para reconstruirlo con una precisión satisfactoria.
Por ejemplo, DCT solo funciona bien en funciones periódicas, y si va a lo grande, probablemente obtendrá un salto gigante en los límites del bloque y necesitará muchos componentes de alta frecuencia para cubrirlo. ¡Esto no es verdad! Esta explicación es muy similar a DFT, pero no a DCT, ya que cubre perfectamente dichos saltos con los primeros componentes.
En la misma página hay una respuesta de las preguntas frecuentes sobre MPEG, con los principales argumentos en contra de los bloques grandes:
Le sugiero que investigue esto usted mismo. Empecemos con primero.
El eje horizontal muestra la proporción de los primeros coeficientes distintos de cero. Vertical: desviación estándar de píxeles del original. La desviación máxima posible se toma como uno. Por supuesto, una imagen claramente no es suficiente para emitir un veredicto. Además, no estoy actuando del todo correctamente, simplemente pongo a cero. En un JPEG real, dependiendo de la matriz de cuantificación, solo se ponen a cero los valores pequeños de los componentes de alta frecuencia. Por lo tanto, los siguientes experimentos y conclusiones pretenden sacar a la luz los principios y patrones.
Puedes comparar la división en diferentes bloques con el 25 por ciento de los coeficientes restantes (de izquierda a derecha, luego de derecha a izquierda): 

Esto significa que, por ejemplo, el cálculo para una partición de 64x64 es dos veces más complejo que el de una partición de 8x8. 
Aunque la distorsión de los bloques de 16x16 se extiende más que la de los de 8x8, las letras son más suaves. Por tanto, sólo los dos primeros argumentos me convencieron. Pero de alguna manera me gusta más la división 16x16.Cuantización
En esta etapa tenemos un montón de matrices de 8x8 con coeficientes de transformada de coseno. Es hora de deshacerse de los coeficientes insignificantes. Existe una solución más elegante que simplemente restablecer los últimos coeficientes a cero, como hicimos anteriormente. No estamos satisfechos con este método, ya que los valores distintos de cero se almacenan con excesiva precisión, y entre los que no tuvieron suerte podría haber otros bastante importantes. La solución es utilizar una matriz de cuantificación. Las pérdidas ocurren precisamente en esta etapa. Cada coeficiente de Fourier se divide por el número correspondiente en la matriz de cuantificación. Veamos un ejemplo. Tomemos el primer bloque de nuestro mapache y realicemos la cuantificación. La especificación JPEG proporciona una matriz estándar: 
La matriz estándar corresponde al 50% de calidad en FastStone e IrfanView. Esta mesa fue elegida en términos de equilibrio entre calidad y relación de compresión. Creo que el valor del coeficiente DC es mayor que el de sus vecinos debido a que el DCT no está normalizado y el primer valor es mayor de lo que debería ser. Los coeficientes de alta frecuencia se vuelven más gruesos debido a su menor importancia. Creo que estas matrices rara vez se utilizan ahora, ya que el deterioro de la calidad se nota claramente. Nadie prohíbe usar tu tabla (con valores del 1 al 255)
Durante la decodificación, ocurre el proceso inverso: los coeficientes cuantificados se multiplican término por término por los valores de la matriz de cuantificación. Pero como redondeamos los valores, no podremos restaurar con precisión los coeficientes de Fourier originales. Cuanto mayor sea el número de cuantificación, mayor será el error. Por tanto, el coeficiente reconstruido es sólo el múltiplo más cercano.
Otro ejemplo: 

Cuando restauremos este bloque, solo obtendremos el valor promedio más el gradiente vertical (debido al valor conservado de -1). Pero solo se almacenan dos valores: 7 y -1. La situación no es mejor con otros bloques, aquí está la imagen restaurada: 
O puede mirar las matrices de cuantificación de varias cámaras.Codificación
Antes de continuar, necesitamos usar ejemplos más simples para comprender cómo podemos comprimir los valores resultantes.
Imagínese una situación en la que su amigo olvidó un papel con una lista en su casa y ahora le pide que se la dicte por teléfono (no existen otros métodos de comunicación).
Lista:
¿Cómo facilitarías tu tarea? No tienes ningún deseo particular de dictar dolorosamente todas estas palabras. Pero sólo hay dos y se repiten. Por lo tanto, simplemente dicta de alguna manera las dos primeras palabras y acepta que a partir de ahora llamará "d9rg3" a la primera palabra y "wfr43gt" a la segunda. Entonces bastará con dictar: 1, 2, 2, 1, 1, 1, 2, 1. 
Codifica ABC.
Es imposible asociar 3 caracteres diferentes (A, B, C) con 2 valores de bits posibles (0 y 1). Y si es así, entonces puedes usar 2 bits por símbolo. Por ejemplo:
La secuencia de bits asociados a un símbolo se denominará código. ABC se codificará así: 000110. 
Codifica AAAAAABC.
Usar 2 bits por carácter A parece un poco derrochador. ¿Qué pasa si intentas esto?
Secuencia codificada: 000000100.
Evidentemente, esta opción no es adecuada, ya que no está claro cómo decodificar los dos primeros bits de esta secuencia: ¿como AA o como C? Es un desperdicio utilizar cualquier separador entre códigos, pensaremos en cómo sortear este obstáculo de otra forma. Entonces, el fallo se debe a que el código de C comienza con el código de A. Pero estamos decididos a codificar A con un bit, incluso si B y C tienen dos cada uno. Basándonos en este deseo, le damos a A el código 0. Entonces los códigos B y C no pueden comenzar con 0. Pero pueden comenzar con 1: 
La secuencia está codificada así: 0000001011. Intenta decodificarla mentalmente. Sólo puedes hacer esto de una manera.
Hemos desarrollado dos requisitos de codificación:
Evidentemente, el orden de los personajes no es importante, sólo nos interesa la frecuencia con la que aparecen. Por tanto, cada símbolo está asociado a un número llamado peso. El peso de un símbolo puede ser un valor relativo, que refleja la proporción de su aparición, o un valor absoluto, igual al número de caracteres. Lo principal es que los pesos son proporcionales a la aparición de símbolos.
Consideremos el caso general de 4 símbolos con cualquier peso.
Sin pérdida de generalidad, pongamos pa ≥ pb ≥ pc ≥ pd. Sólo hay dos opciones que difieren fundamentalmente en la longitud del código: 
¿Cuál es preferible? Para hacer esto, necesita calcular la longitud resultante de los mensajes codificados:
W1 = 2*pa + 2*pb + 2*pc + 2*pd
W2 = pa + 2*pb + 3*pc + 3*pd
Si W1 es menor que W2 (W1-W2<0), то лучше использовать первый вариант:
W1-W2 = pa - (pc+pd)< 0 =>Pensilvania< pc+pd.
Si C y D juntos ocurren con más frecuencia que otros, entonces su vértice común recibe el código de un bit más corto. De lo contrario, un bit va al carácter A. Esto significa que la unión de caracteres se comporta como un carácter independiente y tiene un peso igual a la suma de los caracteres de entrada.
En general, si p es el peso de un carácter representado por la fracción de su aparición (de 0 a 1), entonces la mejor longitud de código es s=-log 2 p.
Consideremos esto en un caso simple (se puede representar fácilmente como un árbol). Entonces, necesitamos codificar 2 caracteres con pesos iguales (1/2 s). Debido a la igualdad de pesos, las longitudes de los códigos serán las mismas. Cada carácter requerirá s bits. Esto significa que si el peso de un símbolo es 1/2 s, entonces su longitud es s. Si reemplazamos el peso con p, obtenemos la longitud del código s=-log 2 p. Esto significa que si un carácter aparece dos veces más que otro, entonces la longitud de su código será un bit más larga. Sin embargo, es fácil llegar a esta conclusión si recuerda que agregar un bit le permite duplicar el número de opciones posibles.
Y una observación más: los dos símbolos con los pesos más pequeños siempre tienen las longitudes de código más grandes pero iguales. Además, sus partes, excepto la última, son las mismas. Si esto no fuera cierto, entonces al menos un código podría acortarse en 1 bit sin romper el prefijo. Esto significa que los dos símbolos con los pesos más pequeños en el árbol de código tienen un padre común en un nivel superior. Puedes ver esto en los ejemplos C y D anteriores.
Intentemos resolver el siguiente ejemplo, basándonos en las conclusiones obtenidas en el ejemplo anterior.
Los pasos se repiten hasta que solo quede un grupo. Dentro de cada grupo, a un carácter (o subgrupo) se le asigna el bit 0 y a otro carácter el bit 1.
Este algoritmo se llama codificación de Huffman.
La ilustración muestra un ejemplo con 5 caracteres (A: 8, B: 6, C: 5, D: 4, E: 3). A la derecha está el peso del símbolo (o grupo). 
Codificamos los coeficientes.
Volvamos. Ahora tenemos muchos bloques con 64 coeficientes en cada uno, que deben guardarse de alguna manera. La solución más sencilla es utilizar un número fijo de bits por coeficiente, lo que evidentemente no resulta exitoso. Construyamos un histograma de todos los valores obtenidos (es decir, la dependencia del número de coeficientes de su valor): 
Tenga en cuenta que la escala es logarítmica. ¿Puede explicar el motivo de la aparición de un grupo de valores superiores a 200? Estos son coeficientes DC. Dado que son muy diferentes de los demás, no es de extrañar que estén codificados por separado. Aquí está solo DC: 
Tenga en cuenta que la forma del gráfico recuerda a los gráficos de los primeros experimentos de emparejamiento y triplicación de píxeles.
En general, los valores del coeficiente DC pueden variar de 0 a 2047 (más precisamente de -1024 a 1023, ya que JPEG resta 128 de todos los valores originales, lo que corresponde a restar 1024 de DC) y se distribuye de manera bastante uniforme con pequeños picos. Entonces la codificación de Huffman no ayudará mucho aquí. ¡E imagina lo grande que será el árbol de codificación! Y durante la decodificación tendrás que buscar significados en él. Es muy costoso. Pensamos más.
El coeficiente DC es el valor promedio de un bloque de 8x8. Imaginemos una transición de gradiente (aunque no ideal), que se encuentra a menudo en las fotografías. Los valores de DC en sí serán diferentes, pero representarán una progresión aritmética. Esto significa que su diferencia será más o menos constante. Construyamos un histograma de diferencias: 
Esto es mejor, porque los valores generalmente se concentran alrededor de cero (pero el algoritmo de Huffman volverá a dar un árbol demasiado grande). Los valores pequeños (en valor absoluto) son comunes, los valores grandes son raros. Y dado que los valores pequeños ocupan pocos bits (si se eliminan los ceros a la izquierda), se sigue bien una de las reglas de compresión: a los símbolos con pesos grandes se les asignan códigos cortos (y viceversa). Actualmente estamos limitados por el incumplimiento de otra regla: la imposibilidad de una decodificación inequívoca. En general, este problema se puede resolver de las siguientes maneras: molestarse con el código delimitador, indicar la longitud del código, usar códigos de prefijo (ya los conoce; este es el caso cuando ningún código comienza con otro). Vayamos con la segunda opción simple, es decir, cada coeficiente (más precisamente, la diferencia entre los vecinos) se escribirá así: (longitud)(valor), según este signo: 
Es decir, los valores positivos se codifican directamente mediante su representación binaria y los valores negativos se codifican de la misma manera, pero con el 1 inicial reemplazado por 0. Queda por decidir cómo codificar las longitudes. Como hay 12 valores posibles, se pueden utilizar 4 bits para almacenar la longitud. Pero aquí es donde es mejor utilizar la codificación Huffman. 
Hay la mayor cantidad de valores con longitudes 4 y 6, por lo que obtuvieron los códigos más cortos (00 y 01).
Puede surgir la pregunta: ¿por qué en el ejemplo el valor 9 tiene el código 1111110 y no 1111111? Después de todo, ¿puedes elevar con seguridad el “9” a un nivel superior, junto al “0”? El hecho es que en JPEG no se puede utilizar un código que consta únicamente de unos; dicho código está reservado.
Hay una característica más. Los códigos obtenidos mediante el algoritmo de Huffman descrito podrán no coincidir en bits con los códigos en formato JPEG, aunque sus longitudes serán las mismas. Usando el algoritmo de Huffman, se obtienen las longitudes de los códigos y se generan los códigos mismos (el algoritmo es simple: comience con códigos cortos y agréguelos uno por uno al árbol lo más a la izquierda posible, conservando la propiedad del prefijo ). Por ejemplo, para el árbol de arriba se almacena la lista: 0,2,3,1,1,1,1,1. Y, por supuesto, se almacena una lista de valores: 4,6,3,5,7,2,8,1,0,9. Durante la decodificación, los códigos se generan de la misma forma.
[Código Huffman para longitud de diferencia de CC (en bits)]
donde DC diff = corriente DC - DC anterior
Dado que el gráfico es muy similar al gráfico de diferencias de CC, el principio es el mismo: [código Huffman para longitud de CA (en bits)]. ¡Pero no realmente! Dado que la escala del gráfico es logarítmica, no se nota inmediatamente que hay aproximadamente 10 veces más valores cero que valores 2, el siguiente en frecuencia. Esto es comprensible: no todos sobrevivieron a la cuantificación. Volvamos a la matriz de valores obtenidos durante la etapa de cuantificación (utilizando la matriz de cuantificación FastStone, 90%). 
Dado que hay muchos grupos de ceros consecutivos, surge una idea: anotar solo el número de ceros en el grupo. Este algoritmo de compresión se llama RLE (codificación de longitud de ejecución). Queda por descubrir la dirección de la derivación de los "consecutivos": ¿quién está detrás de quién? Escribir de izquierda a derecha y de arriba a abajo no es muy efectivo, ya que los coeficientes distintos de cero se concentran cerca de la esquina superior izquierda, y cuanto más cerca de la esquina inferior derecha, más ceros. 
Por lo tanto, JPEG utiliza un orden llamado "Zig-zag", que se muestra en la figura de la izquierda. Este método distingue bien grupos de ceros. En la imagen de la derecha hay un método de bypass alternativo, no relacionado con JPEG, pero con un nombre curioso (prueba). Se puede utilizar en MPEG para compresión de vídeo entrelazado. La elección del algoritmo transversal no afecta la calidad de la imagen, pero puede aumentar la cantidad de grupos de ceros codificados, lo que en última instancia puede afectar el tamaño del archivo.
Modifiquemos nuestra entrada. Para cada coeficiente AC distinto de cero:
[Número de ceros antes de AC][Código Huffman para longitud de AC (en bits)]
¡Creo que puedes darte cuenta de inmediato que Huffman también codifica perfectamente el número de ceros! Esta es una respuesta muy cercana y buena. Pero se puede optimizar un poco. Imaginemos que tenemos algún coeficiente AC, delante del cual había 7 ceros (por supuesto, si se escribe en zigzag). Estos ceros son el espíritu de valores que no sobrevivieron a la cuantización. Lo más probable es que nuestro coeficiente también haya resultado gravemente dañado y se haya vuelto pequeño, lo que significa que su longitud es corta. Esto significa que el número de ceros delante de AC y la longitud de AC son cantidades dependientes. Por eso lo escribimos así:
[Código Huffman para (Número de ceros antes de AC, longitud de AC (en bits)]
El algoritmo de codificación sigue siendo el mismo: aquellos pares (número de ceros antes de AC, longitud de AC) que aparecen con frecuencia recibirán códigos cortos y viceversa. 
La larga “cresta montañosa” confirma nuestra suposición.
Un par de este tipo ocupa 1 byte: 4 bits para el número de ceros y 4 bits para la longitud de AC. 4 bits son valores del 0 al 15. Para la longitud de AC esto es más que suficiente, pero ¿puede haber más de 15 ceros? Luego se utilizan más pares. Por ejemplo, para 20 ceros: (15, 0)(5, AC). Es decir, el decimosexto cero se codifica como un coeficiente distinto de cero. Como siempre hay muchos ceros cerca del final del bloque, el par (0,0) se utiliza después del último coeficiente distinto de cero. Si se encuentra durante la decodificación, los valores restantes son 0.
[Código Huffman para longitud de diferenciación de CC]
[Código Huffman para (número de ceros antes de AC 1, longitud de AC 1]
…
[Código Huffman para (número de ceros antes de AC n, longitud de AC n]
Donde AC i son coeficientes AC distintos de cero.Imagen en color
La forma en que se representa una imagen en color depende del modelo de color seleccionado. Una solución sencilla es utilizar RGB y codificar cada canal de color de la imagen por separado. Entonces la codificación no será diferente de codificar una imagen gris, solo 3 veces más trabajo. Pero la compresión de la imagen se puede aumentar si recordamos que el ojo es más sensible a los cambios de brillo que a los colores. Esto significa que el color se puede almacenar con mayores pérdidas que el brillo. RGB no tiene un canal de brillo separado. Depende de la suma de los valores de cada canal. Por lo tanto, el cubo RGB (esta es una representación de todos los valores posibles) simplemente se "coloca" en la diagonal: cuanto más alto, más brillante. Pero no se detienen ahí: el cubo se presiona un poco por los lados y resulta más como un paralelepípedo, pero esto es solo para tener en cuenta las características del ojo. Por ejemplo, es más sensible al verde que al azul. Así surgió el modelo YCbCr. 
(Imagen de Intel.com)
Y es el componente de luminancia, Cb y Cr son los componentes de diferencia de color azul y rojo. Por lo tanto, si quieren comprimir más la imagen, entonces RGB se convierte a YCbCr y los canales Cb y Cr se adelgazan. Es decir, se dividen en pequeños bloques, por ejemplo 2x2, 4x2, 1x2, y se promedian todos los valores de un bloque. O, en otras palabras, reducen el tamaño de la imagen de este canal 2 o 4 veces en vertical y/u horizontal. 
Cada bloque de 8x8 está codificado (DCT + Huffman) y las secuencias codificadas se escriben en este orden:
Es curioso que la especificación JPEG no limite la elección del modelo, es decir, la implementación del codificador puede dividir la imagen en componentes de color (canales) de cualquier forma y cada uno se guardará por separado. Conozco el uso de escala de grises (1 canal), YCbCr (3), RGB (3), YCbCrK (4), CMYK (4). Los tres primeros son compatibles con casi todos, pero hay problemas con los últimos 4 canales. FastStone, GIMP los admiten correctamente y los programas estándar de Windows, paint.net, extraen correctamente toda la información, pero luego descartan el cuarto canal negro, por lo tanto (Antelle dijo que no lo tiran, lea sus comentarios) muestran un encendedor. imagen. A la izquierda hay un JPEG YCbCr clásico, a la derecha hay un JPEG CMYK: 

Si difieren en color, o solo se ve una imagen, lo más probable es que tengas IE (cualquier versión) (UPD. en los comentarios dicen "o Safari"). Puede intentar abrir el artículo en diferentes navegadores. Y una cosa más
En pocas palabras, sobre funciones adicionales. Modo progresivo
Descompongamos las tablas resultantes de coeficientes DCT en la suma de las tablas (aproximadamente así (DC, -19, -22, 2, 1) = (DC, 0, 0, 0, 0) + (0, -20 , -20, 0, 0) + (0, 1, -2, 2, 1)). Primero codificamos todos los primeros términos (como ya hemos aprendido: Huffman y recorrido en zigzag), luego el segundo, etc. Este truco es útil cuando Internet es lento, ya que primero solo se cargan los coeficientes DC, que se utilizan para construya una imagen aproximada con “píxeles” de 8x8. Luego se redondearon los coeficientes AC para refinar la figura. Luego correcciones aproximadas, luego correcciones más precisas. Etcétera. Los coeficientes están redondeados, ya que en las primeras etapas de la carga la precisión no es tan importante, pero el redondeo tiene un efecto positivo en la longitud de los códigos, ya que cada etapa utiliza su propia tabla de Huffman. Modo sin pérdidas
Compresión sin perdidas. Sin DCT. Se utiliza la predicción del cuarto punto en base a tres vecinos. Los errores de predicción están codificados por Huffman. En mi opinión, se utiliza un poco más a menudo que nunca. Modo jerárquico
A partir de la imagen se crean varias capas con diferentes resoluciones. La primera capa gruesa se codifica como de costumbre, y luego solo la diferencia (refinamiento de la imagen) entre las capas (pretendida como una wavelet de Haar). DCT o Lossless se utiliza para la codificación. En mi opinión, se utiliza con menos frecuencia que nunca. Codificación aritmética
El algoritmo de Huffman produce códigos óptimos basados en el peso de los caracteres, pero esto sólo es cierto para una asignación fija de carácter a código. La aritmética no tiene una vinculación tan rígida, lo que permite el uso de códigos como si tuvieran un número fraccionario de bits. Afirma reducir el tamaño del archivo en un promedio del 10% en comparación con Huffman. No está muy extendido debido a cuestiones de patentes y no todos lo apoyan.
vanwin sugirió indicar el software utilizado. Me complace anunciar que todo está disponible y es gratuito:




 .
.




