Programación lineal en excel en la práctica. Problemas de programación lineal, solución mediante MS Excel. Problema de planificación de la producción de pintura.
Los principales indicadores generalizadores de variación en las estadísticas son las dispersiones y las desviaciones estándar.
Dispersión esto media aritmética desviaciones al cuadrado de cada valor característico del promedio general. La varianza generalmente se denomina cuadrado medio de las desviaciones y se denota por 2. Dependiendo de los datos de origen, la varianza se puede calcular utilizando la media aritmética simple o ponderada:
varianza no ponderada (simple);
 varianza ponderada.
varianza ponderada.
Desviación estándar esta es una característica generalizadora de los tamaños absolutos variaciones signos en conjunto. Se expresa en las mismas unidades de medida que el atributo (en metros, toneladas, porcentaje, hectáreas, etc.).
La desviación estándar es la raíz cuadrada de la varianza y se denota por :
 desviación estándar no ponderada;
desviación estándar no ponderada;
 desviación estándar ponderada.
desviación estándar ponderada.
La desviación estándar es una medida de la confiabilidad de la media. Cuanto menor sea la desviación estándar, mejor refleja la media aritmética a toda la población representada.
El cálculo de la desviación estándar va precedido del cálculo de la varianza.
El procedimiento para calcular la varianza ponderada es el siguiente:
1) determinar la media aritmética ponderada:
2) calcular las desviaciones de las opciones del promedio:
3) eleva al cuadrado la desviación de cada opción del promedio:
4) multiplicar los cuadrados de las desviaciones por pesos (frecuencias):
5) resumir los productos resultantes:
![]()
6) la cantidad resultante se divide por la suma de los pesos:

Ejemplo 2.1

Calculemos la media aritmética ponderada:

Los valores de las desviaciones de la media y sus cuadrados se presentan en la tabla. Definamos la varianza:

La desviación estándar será igual a:

Si los datos de origen se presentan en forma de intervalo serie de distribución , primero debe determinar el valor discreto del atributo y luego aplicar el método descrito.
Ejemplo 2.2
Muestremos el cálculo de la varianza para una serie de intervalos utilizando datos sobre la distribución del área sembrada de una finca colectiva según el rendimiento del trigo.

La media aritmética es:

Calculemos la varianza:

6.3. Cálculo de la varianza mediante una fórmula basada en datos individuales.
Técnica de cálculo variaciones complicado, pero valores grandes Las opciones y frecuencias pueden ser abrumadoras. Los cálculos se pueden simplificar utilizando las propiedades de dispersión.
La dispersión tiene las siguientes propiedades.
1. Reducir o aumentar los pesos (frecuencias) de una característica variable un cierto número de veces no cambia la dispersión.
2. Disminuir o aumentar cada valor de una característica en la misma cantidad constante A no cambia la dispersión.
3. Disminuir o aumentar cada valor de una característica un cierto número de veces. k respectivamente reduce o aumenta la varianza en k 2 veces y desviación estándar en k una vez.
4. La dispersión de una característica con respecto a un valor arbitrario es siempre mayor que la dispersión con respecto a la media aritmética por cuadrado de la diferencia entre los valores promedio y arbitrarios:
![]()
Si A 0, entonces llegamos a la siguiente igualdad:
es decir, la varianza de la característica es igual a la diferencia entre el cuadrado medio de los valores característicos y el cuadrado de la media.
Cada propiedad se puede utilizar de forma independiente o en combinación con otras al calcular la varianza.
El procedimiento para calcular la varianza es simple:
1) determinar media aritmética :
2) eleva al cuadrado la media aritmética:

3) elevar al cuadrado la desviación de cada variante de la serie:
incógnita i 2 .
4) encuentra la suma de cuadrados de las opciones:
5) dividir la suma de los cuadrados de las opciones por su número, es decir determinar el cuadrado promedio:
6) determinar la diferencia entre el cuadrado medio de la característica y el cuadrado de la media:
Ejemplo 3.1 Se dispone de los siguientes datos sobre la productividad de los trabajadores:

Hagamos los siguientes cálculos:
![]()
Expectativa matemática (valor medio) variable aleatoria X dado en un espacio de probabilidad discreto se llama número m =M[X]=∑x i p i si la serie converge absolutamente.
Objeto del servicio. Usando el servicio en modo en línea Se calculan la expectativa matemática, la varianza y la desviación estándar.(ver ejemplo). Además, se traza una gráfica de la función de distribución F(X).
Propiedades de la expectativa matemática de una variable aleatoria.
- Expectativa valor constante igual a sí mismo: M[C]=C, C es una constante;
- M=C M[X]
- La expectativa matemática de la suma de variables aleatorias es igual a la suma de sus expectativas matemáticas: M=M[X]+M[Y]
- La expectativa matemática del producto de variables aleatorias independientes es igual al producto de sus expectativas matemáticas: M=M[X] M[Y] , si X e Y son independientes.
Propiedades de dispersión
- La varianza de un valor constante es cero: D(c)=0.
- El factor constante se puede sacar del signo de dispersión elevándolo al cuadrado: D(k*X)= k 2 D(X).
- Si las variables aleatorias X e Y son independientes, entonces la varianza de la suma es igual a la suma de las varianzas: D(X+Y)=D(X)+D(Y).
- Si las variables aleatorias X e Y son dependientes: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- La siguiente fórmula computacional es válida para la dispersión:
D(X)=M(X 2)-(M(X)) 2
Ejemplo. Se conocen las expectativas matemáticas y las varianzas de dos variables aleatorias independientes X e Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Encuentre la expectativa matemática y la varianza de la variable aleatoria Z=9X-8Y+7.
Solución. Basado en las propiedades de la expectativa matemática: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Basado en las propiedades de dispersión: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algoritmo para calcular la expectativa matemática.
Propiedades de variables aleatorias discretas: todos sus valores se pueden renumerar números naturales; Asigne a cada valor una probabilidad distinta de cero.- Multiplicamos los pares uno a uno: x i por p i .
- Suma el producto de cada par x i p i .
Por ejemplo, para n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Ejemplo No. 1.
| xyo | 1 | 3 | 4 | 7 | 9 |
| p yo | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Encontramos la expectativa matemática usando la fórmula m = ∑x i p i .
Expectativa M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Encontramos la varianza usando la fórmula d = ∑x 2 i p i - M[x] 2 .
Varianza D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Desviación estándar σ(x).
σ = raíz cuadrada (D[X]) = raíz cuadrada (7,69) = 2,78
Ejemplo No. 2. Una variable aleatoria discreta tiene la siguiente serie de distribución:
| incógnita | -10 | -5 | 0 | 5 | 10 |
| r | A | 0,32 | 2a | 0,41 | 0,03 |
Solución. El valor de a se encuentra a partir de la relación: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0,76 + 3 a = 1 o 0,24=3 a , de donde a = 0,08
Ejemplo No. 3. Determine la ley de distribución de una variable aleatoria discreta si se conoce su varianza y x 1
p1 = 0,3; p2 = 0,3; p3 = 0,1; p 4 = 0,3
d(x)=12,96
Solución.
Aquí necesitas crear una fórmula para encontrar la varianza d(x):
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
donde expectativa m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Para nuestros datos
metro(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
o -9/100 (x 2 -20x+96)=0
En consecuencia, necesitamos encontrar las raíces de la ecuación, y habrá dos.
x 3 = 8, x 3 = 12
Elige el que cumpla la condición x 1
Ley de distribución de una variable aleatoria discreta.
x1 =6; x2=9; x3 =12; x4=15
p1 = 0,3; p2 = 0,3; p3 = 0,1; p 4 = 0,3
Donde σ 2 j es la varianza intragrupo del jésimo grupo.
Para datos desagrupados varianza residual– medida de la precisión de la aproximación, es decir aproximación de la línea de regresión a los datos originales: 
donde y(t) – pronóstico según la ecuación de tendencia; y t – serie dinámica inicial; n – número de puntos; p – número de coeficientes de la ecuación de regresión (número de variables explicativas).
En este ejemplo se llama estimador de varianza insesgado.
Ejemplo No. 1. La distribución de los trabajadores de tres empresas de una asociación según categorías arancelarias se caracteriza por los siguientes datos:
| Categoría arancelaria del trabajador | Número de trabajadores en la empresa. | ||
| empresa 1 | empresa 2 | empresa 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Definir:
1. variación para cada empresa (variaciones intragrupo);
2. el promedio de las variaciones dentro del grupo;
3. varianza intergrupal ;
4. variación total.
Solución.
Antes de empezar a solucionar el problema, es necesario averiguar qué característica es efectiva y cuál es factorial. En el ejemplo que nos ocupa, el atributo resultante es “Categoría arancelaria” y el atributo del factor es “Número (nombre) de la empresa”.
Luego tenemos tres grupos (empresas), para los cuales es necesario calcular el promedio del grupo y las variaciones intragrupo:

| Empresa | promedio del grupo, | Variación dentro del grupo, |
| 1 | 4 | 1,8 |
El promedio de las varianzas dentro del grupo ( varianza residual) se calculará mediante la fórmula:
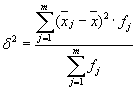
donde puedes calcular:

o:

Entonces:
La varianza total será igual a: s 2 = 1,6 + 0 = 1,6.
La varianza total también se puede calcular utilizando una de las dos fórmulas siguientes:

Al resolver problemas prácticos, a menudo uno tiene que lidiar con una característica que toma sólo dos valores alternativos. En este caso, no estamos hablando del peso de un valor particular de una característica, sino de su participación en la totalidad. Si la proporción de unidades de población que poseen la característica que se está estudiando se denota por " r", y los que no tienen - a través de " q", entonces la varianza se puede calcular usando la fórmula:
s2 = p×q
Ejemplo No. 2. Con base en los datos de producción de seis trabajadores en un equipo, determine la varianza intergrupal y evalúe el impacto del turno de trabajo en su productividad laboral si la varianza total es 12,2.
| Trabajador del equipo no. | Producción de trabajadores, uds. | |
| en el primer turno | en el segundo turno | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Solución. Datos iniciales
| incógnita | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | Total |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Total | 31 | 33 | 37 | 37 | 40 | 38 |
Luego tenemos 6 grupos para los cuales es necesario calcular la media grupal y las varianzas intragrupo.
1. Encuentra los valores promedio de cada grupo..
2. Encuentra el cuadrado medio de cada grupo..
Resumamos los resultados del cálculo en una tabla:
| Número de grupo | Promedio del grupo | Variación dentro del grupo |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Variación dentro del grupo caracteriza el cambio (variación) de la característica estudiada (resultante) dentro de un grupo bajo la influencia de todos los factores sobre él, excepto el factor subyacente a la agrupación:
El promedio de las variaciones intragrupo se calculará mediante la fórmula:
4. Varianza intergrupal caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de un factor (característica factorial) que forma la base del grupo.
Definimos la varianza intergrupal como:
Dónde
Entonces
varianza total caracteriza el cambio (variación) de la característica estudiada (resultante) bajo la influencia de todos los factores (características factoriales) sin excepción. Según las condiciones del problema, es igual a 12,2.
Relación de correlación empírica Mide qué parte de la variabilidad total de la característica resultante es causada por el factor que se está estudiando. Esta es la relación entre la varianza del factor y la varianza total:
Definimos la relación de correlación empírica:
Las conexiones entre características pueden ser débiles y fuertes (estrechas). Sus criterios se evalúan según la escala de Chaddock:
0,1 0,3 0,5 0,7 0,9 En nuestro ejemplo, la relación entre el rasgo Y y el factor X es débil
Coeficiente de determinación.
Determinemos el coeficiente de determinación:
Así, el 0,67% de la variación se debe a diferencias entre rasgos, y el 99,37% se debe a otros factores.
Conclusión: en este caso, la producción de los trabajadores no depende del trabajo en un turno específico, es decir la influencia del turno de trabajo en su productividad laboral no es significativa y se debe a otros factores.
Ejemplo No. 3. Con base en los datos sobre los salarios promedio y las desviaciones al cuadrado de su valor para dos grupos de trabajadores, encuentre la varianza total aplicando la regla de sumar varianzas:
Solución:Promedio de variaciones dentro del grupo
Definimos la varianza intergrupal como:
La varianza total será: 480 + 13824 = 14304
calculemos enEMSOBRESALIRvarianza muestral y desviación estándar. También calcularemos la varianza de una variable aleatoria si se conoce su distribución.
Consideremos primero dispersión, entonces desviación estándar.
varianza muestral
varianza muestral (varianza de la muestra,muestradiferencia) caracteriza la dispersión de valores en la matriz en relación con .
Las 3 fórmulas son matemáticamente equivalentes.
De la primera fórmula queda claro que varianza muestral es la suma de las desviaciones al cuadrado de cada valor en la matriz del promedio, dividido por el tamaño de la muestra menos 1.
variaciones muestras Se utiliza la función DISP(), en inglés. el nombre VAR, es decir Diferencia. A partir de la versión MS EXCEL 2010, se recomienda utilizar su análogo DISP.V(), inglés. el nombre VARS, es decir Varianza de la muestra. Además, a partir de la versión de MS EXCEL 2010, existe la función DISP.Г(), en inglés. el nombre VARP, es decir VARIanza poblacional, que calcula dispersión Para población. Toda la diferencia se reduce al denominador: en lugar de n-1 como DISP.V(), DISP.G() tiene solo n en el denominador. Antes de MS EXCEL 2010, la función VAR() se utilizaba para calcular la varianza de la población.
varianza muestral
=QUADROTCL(Muestra)/(CONTAR(Muestra)-1)
=(SUM(Muestra)-COUNT(Muestra)*PROMEDIO(Muestra)^2)/ (COUNT(Muestra)-1)– fórmula habitual
=SUM((Muestra -PROMEDIO(Muestra))^2)/ (CONTAR(Muestra)-1) –
varianza muestral es igual a 0, solo si todos los valores son iguales entre sí y, en consecuencia, iguales valor promedio. Por lo general, cuanto mayor sea el valor variaciones, mayor será la dispersión de valores en la matriz.
varianza muestral es una estimación puntual variaciones distribución de la variable aleatoria a partir de la cual se hizo muestra. Sobre la construcción intervalos de confianza al evaluar variaciones se puede leer en el artículo.
Varianza de una variable aleatoria
para calcular dispersión variable aleatoria, necesitas saberla.
Para variaciones La variable aleatoria X a menudo se denomina Var(X). Dispersión igual al cuadrado de la desviación de la media E(X): Var(X)=E[(X-E(X)) 2 ]
dispersión calculado por la fórmula:

donde x i es el valor que puede tomar una variable aleatoria y μ es el valor promedio (), p(x) es la probabilidad de que la variable aleatoria tome el valor x.
Si una variable aleatoria tiene , entonces dispersión calculado por la fórmula:

Dimensión variaciones Corresponde al cuadrado de la unidad de medida de los valores originales. Por ejemplo, si los valores de la muestra representan medidas de peso de las piezas (en kg), entonces la dimensión de la varianza sería kg 2 . Esto puede ser difícil de interpretar, por lo que para caracterizar la dispersión de valores, un valor igual a la raíz cuadrada de variaciones – desviación estándar.
Algunas propiedades variaciones:
Var(X+a)=Var(X), donde X es una variable aleatoria y a es una constante.
Var(aХ)=a 2 Var(X)
Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Esta propiedad de dispersión se utiliza en artículo sobre regresión lineal.
Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), donde X e Y son variables aleatorias, Cov(X;Y) es la covarianza de estas variables aleatorias.
Si las variables aleatorias son independientes, entonces covarianza es igual a 0, y por lo tanto Var(X+Y)=Var(X)+Var(Y). Esta propiedad de dispersión se utiliza en la derivación.
Demostremos que para cantidades independientes Var(X-Y)=Var(X+Y). De hecho, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Esta propiedad de dispersión se utiliza para construir.
Desviación estándar muestral
Desviación estándar muestral es una medida de qué tan dispersos están los valores en una muestra en relación con sus .
Por definición, desviación estándar igual a la raíz cuadrada de variaciones:

Desviación estándar no tiene en cuenta la magnitud de los valores en muestra, pero solo el grado de dispersión de valores a su alrededor. promedio. Para ilustrar esto, pongamos un ejemplo.
Calculemos la desviación estándar para 2 muestras: (1; 5; 9) y (1001; 1005; 1009). En ambos casos, s=4. Es obvio que la relación entre la desviación estándar y los valores de la matriz difiere significativamente entre muestras. Para tales casos se utiliza Coeficiente de variación(Coeficiente de variación, CV) - relación Desviación estándar al promedio aritmética, expresado como porcentaje.
En MS EXCEL 2007 y versiones anteriores para cálculo Desviación estándar muestral se utiliza la función =STDEVAL(), en inglés. nombre STDEV, es decir Desviación estándar. A partir de la versión de MS EXCEL 2010, se recomienda utilizar su análogo =STDEV.B() , en inglés. nombre STDEV.S, es decir Muestra de desviación estándar.
Además, a partir de la versión de MS EXCEL 2010, existe una función STANDARDEV.G(), en inglés. nombre STDEV.P, es decir Desviación estándar de la población, que calcula desviación estándar Para población. Toda la diferencia se reduce al denominador: en lugar de n-1 como en STANARDEV.V(), STANARDEVAL.G() tiene solo n en el denominador.
Desviación estándar También se puede calcular directamente usando las fórmulas siguientes (ver archivo de ejemplo)
=RAÍZ(QUADROTCL(Muestra)/(CONTAR(Muestra)-1))
=RAÍZ((SUM(Muestra)-CONTAR(Muestra)*PROMEDIO(Muestra)^2)/(CONTAR(Muestra)-1))
Otras medidas de dispersión
La función SQUADROTCL() calcula con una suma de desviaciones al cuadrado de los valores de sus promedio. Esta función devolverá el mismo resultado que la fórmula =DISP.G( Muestra)*CONTROLAR( Muestra) , Dónde Muestra- una referencia a un rango que contiene una matriz de valores de muestra (). Los cálculos en la función QUADROCL() se realizan según la fórmula:

La función SROTCL() también es una medida de la dispersión de un conjunto de datos. La función SROTCL() calcula el promedio de los valores absolutos de las desviaciones de valores de promedio. Esta función devolverá el mismo resultado que la fórmula. =SUMAPRODUCTO(ABS(Muestra-PROMEDIO(Muestra)))/CONTAR(Muestra), Dónde Muestra- un enlace a un rango que contiene una serie de valores de muestra.
Los cálculos en la función SROTCL () se realizan según la fórmula:





