Алгоритм JPEG является алгоритмом сжатия данных с потерями. Алгоритмы архивации с потерями
Фотографии и картинки отличаются друг от друга не только по содержанию, но и по другим «компьютерным» характеристикам. Например, по размеру.
Бывает так, что, вроде бы, два одинаковых рисунка, но у одного размер в три раза больше, чем у другого.
Также изображения отличаются по качеству. Думаю, Вам не раз встречались фото крайне плохого качества. Это видно невооруженным глазом. Например, две одинаковые фотографии, но одна лучшего качества, а другая - худшего.
А бывает так, что рисунку как будто не хватает красок. Вот пример.

И за все это отвечает формат или тип файла.
Вообще-то изображения бывают самых разных форматов. И существует их очень и очень много. Мы не будем рассматривать их все, а поговорим про самые распространенные. Это такие форматы, как bmp, gif, jpg, png, tiff .
Отличаются он друг от друга, в первую очередь, качеством. А качество отличается по количеству (насыщенности) цветов.
Например, я рисую картину, используя разные цвета . И тут вдруг часть из них закончилась, и приходится дорисовывать тем, что есть. Я, конечно, постараюсь сделать всё возможное, чтобы это не сильно отразилось на результате, но все равно картина получится не такая, как хотелось бы - более блеклая, размытая.
Вот так и с форматами изображений. Какой-то оставляет все цвета, другой же обрезает часть. И, бывает, из-за этого картинка портится.
Это довольно грубый пример. На самом деле, там все несколько сложнее, но, думаю, главное Вы уловили.
Распространенные форматы изображений
BMP - формат рисунков, сделанных в программе Paint . Его можно использовать для хранения нарисованных картинок на компьютере. Но вот в Интернете такой тип файлов не используется из-за большого объема. Так что если Вы хотите опубликовать картинку, нарисованную в Paint, в блоге или социальной сети , она должна быть другого типа - gif, jpg или png.
GIF - популярный формат картинок в Интернете. В нем можно сохранять их без потери качества, но с ограниченным количеством цветов - 256. Особую популярность gif получил благодаря тому, что в нем можно создать небольшие анимированные (движущиеся) картинки.
JPG - формат фотографий и картин с большим количеством цветов. В нем можно сохранить изображение как без потери качества, так и с потерей.
PNG - современный формат рисунков. Изображение такого типа получается небольшого размера и без потери качества. Очень удобно: и файл маленький, и качество хорошее. А еще он поддерживает прозрачность.
TIFF - изображения очень хорошего качества, без сжатия.Соответственно, и размер у таких файлов огромный. TIFF используют тогда, когда качество имеет большое значение. Например, при создании визиток, буклетов, журнальных обложек.
Какой формат выбрать
- BMP - если это рисунок, сделанный в программе Paint, и Вы собираетесь держать его только в компьютере.
- GIF - если анимация или рисунок с небольшим количеством цветов для публикации в Интернете.
- PNG - если это рисунок, в котором много цветов или есть какие-то прозрачные части.
- JPG (jpeg) - если фотография.
- TIFF - изображение для полиграфии (визитки, буклеты, плакаты и т.д.).
Здравствуйте, уважаемые друзья. Сегодня поговорим о том, какой формат изображения лучше использовать на сайте, какие сегодня доступны форматы графических файлов для сайта и нужно ли гнаться за новинками графических форматов.
Таких вопросов я получаю довольно много, многие из моих учеников спрашивают можно ли им использовать новые форматы SVG и WebP, и где лучше применить эти изображения. Разумеется, можно использовать и новые форматы, только нужно понимать какой формат и для чего подходит лучше.
На сегодняшний день изображения на сайте являются неотъемлемой частью. Начиная от графического дизайна и закачивая изображениями в статьях, графика сопровождает большинство сайтов в сети. Но за красоту приходится расплачиваться
Не оптимизированные изображения являются одним из факторов замедления сайта, на что указывают сервисы проверки.
Поэтому вы будете всегда перед выбором, какой формат выбрать для изображения. От этого будет зависеть его размер и качество. А чтобы использовать изображения меньшего размера и без потери качества, вы должны знать некоторые вещи.
Какие изображения для сайтов использую сегодня
Все изображения для сайтов, подразделяются:
- растровые (пример - JPG, JPEG, GIF, PNG),
- векторные (пример - SVG).
Растровые изображения состоят из пикселей, в которых хранится цвет и значение прозрачности. Такими форматами представлены изображения в статьях, кнопками, иконками и элементами дизайна. Эти изображения популярны среди разработчиков и владельцев сайтов. Основной минус растровых изображений – они плохо масштабируются.
То есть при увеличении размера картинки, идёт потеря качества.

Векторные изображения состоят из линий и точек маршрутов. Информация об изображении хранится в математических инструкциях по отрисовке, что позволяет масштабировать такие изображения сколько угодно без потери качества.
Все эти изображения могут и используются на современных сайтах. Только нужно понимать, что перед загрузкой на сайт, !
Описание популярных форматов изображения для сайта
Из описания этих форматов вы поймёте, где и какой формат применять лучше всего на сайте.
JPEG
JPEG или JPG – один из самых популярных форматов изображений для сайтов. Формат поддерживает миллионы цветов, что и даёт ему лидирующую позицию в представлении фотографий и картинок на сайте.
Изображения в этом формате достаточно хорошо оптимизируются практически без потери качества, что позволяет получить файл меньшего размера без визуальной потери качества. Следует помнить, что каждая последующая оптимизация снижает качество.
Файлы этого формата поддерживаются всем устройствами и браузерами, что ещё раз подтверждает его популярность и позволяет не беспокоиться за проблемы с отображением на сайтах.
Большим недостатком этого формата является отсутствие прозрачности. То есть, комбинировать изображения в таком формате не получится. Для таких задач лучше использовать следующий формат.
PNG
Этот формат использует алгоритм сжатия без потери качества. По количеству цветов и уровню прозрачности доступен в двух видах 8 и 24-бит. Оба поддерживают прозрачность.
8-битный пользуется малой популярностью, а вот 24-битный широко используется для различных изображений на сайте. За счёт прозрачности позволяет создавать комбинированные изображения. Часто используется для создания анимированных кнопок, иконок, где необходим эффект прозрачности.
Изображения в формате PNG можно много раз оптимизировать, редактировать – оно сохранит первоначальное качество.
Формат также поддерживается всеми браузерами и устройствами, что гарантирует его отображение на любом экране.
По качеству изображения выглядят лучше, чем JPG, но вес файла будет больше. Это нужно учитывать при размещении файлов на сайте.
GIF
Это 8-битный формат, поддерживающий 256 цветов, прозрачность и анимацию. За счёт поддержки малого количества цветов, вес файла тоже минимальный.
Формат не подходит для фотографий и изображений с широким диапазоном цветов.
Зато широко используется при создании, баннеров, кнопок, иконок и так далее.
В современных сайтах этот формат используется всё реже.
Далее поговорим об относительно свежих форматах SVG и WebP, которые не так популярны, но набирают популярность и поддержку, и как нельзя лучше подходят под требования скорости загрузки и адаптивности сайтов.
SVG
Это формат векторных файлов на основе XML. Формат стал набирать популярность совсем недавно, так как ранее он слабо поддерживался в браузерах. И из-за проблем отображения никто не торопился его использовать.
На сегодняшний день SVG поддерживается всеми современными браузерами. Но, проблемы с отображением все, же встречаются.
Наиболее часто используют этот формат для простых изображений, таких как логотипы, элементы дизайна и так далее. Неприменим для фотографий.
Формат SVG имеет малый вес, отлично масштабируются, обеспечивая чёткость изображения на любом разрешении экрана, поддерживает анимацию, можно управлять через CSS и размещать в HTML, сокращая количество запросов.
WebP
Формат с открытым исходным кодом, разработан Google специально для интернета. Сегодня YouTube использует преобразование миниатюр для видео в формат WebP.

Формат обеспечивает превосходное сжатие и поддерживает прозрачность. Он сочетает в себе преимущества JPG и PNG форматов без увеличения размера файла.
Но, несмотря на преимущества формата, он поддерживается не всем браузерами, например, IE, Edge, Firefox и Safari.
Существуют способы обхода этих ограничений, но они не дают использовать формат повсеместно.
Заключение
Друзья, надеюсь, объяснил всё понятно, и вы теперь знаете, какой формат изображений лучше использовать на сайте, и почему я не настаиваю на использовании одного какого-то формата, а рекомендую комплексный подход.
Возможно, когда WebP получит широкую поддержку, мы все перейдём на него и заменим jpg и png на своих сайтах.
Давайте обсудим в комментариях, какие вы используете форматы на своих сайтах, что нравится и что не нравится.
На сегодня у меня всё, жду ваших комментариев.
С уважением, Максим Зайцев.
- 1-битный цвет (21 = 2 цвета) бинарный цвет, чаще всего представляется чёрным и белым цветами (или черный и зелёный)
- 2-битный цвет (22 = 4 цвета) CGA, градации серого цвета NeXTstation
- 3-битный цвет (23 = 8 цветов) множество устаревших персональных компьютеров с TV-выходом
- 4-битный цвет (24 = 16 цветов) известен как EGA и в меньшей степени как VGA-стандарт с высоким разрешением
- 5-битный цвет (25 = 32 цвета) Original Amiga chipset
- 6-битный цвет (26 = 64 цвета) Original Amiga chipset
- 8-битный цвет (28 = 256 цветов) Устаревшие Unix- рабочие станции, VGA низкого разрешения, Super VGA, AGA
- 12-битный цвет (212 = 4,096 цветов) некоторые Silicon Graphics-системы, цвет NeXTstation-систем, и Amiga- систем HAM-режима.
- Алгоритмы сжатия без потерь;
- Алгоритмы сжатия с потерями.
С амыми популярными являются три формата файлов – JPEG, RAW, TIFF. Порой можно слышать разногласия среди фотографов – какой же формат файла для фотографии лучше, в каком формате лучше делать снимки, ведь современные фотоаппараты позволяют делать фо тографии в любом из этих форматов, а порой и сразу в нескольких одновременно!
Формат файла, в котором хранится изображение - это, по сути, определенный компромисс между качеством изображения и размером файла.
Наверное вы уже знаете о том, что растровое изображение состоит из пикселей. Как организован растровый файл и в каком виде в нем хранится информация о пикселях и определяет формат файла. Качество изображения для растрового файла определяется двумя основными параметрами: размером пикселя (то есть общим количеством пикселей) и точностью передачи реального цвета цветом пикселя. С размером пикселя понятно – чем больше пикселей (или – чем «мельче» пиксель), тем лучше. А точность передачи цвета зависит от количества цветов на пиксель или глубиной цвета.
Глубина цвета (качество цветопередачи, битность изображения) - объём памяти в количестве бит, используемых для хранения и представления цвета при кодировании одного пикселя растровой графики или видеоизображения. Количество бит говорит о количестве градаций (тональных ступеней) в каждой цветовой составляющей или, просто – о количестве цветов. Добавление 1 бита – это добавление еще одного разряда в двоичном коде цветности.



Например, мы работаем в цветовом пространстве RGB. Значит, есть три канала, из которых образуется итоговый цвет пикселя: красный канал (Rad), зеленый канал (Green), синий канал (Blue). Предположим, каналы четырехбитные. Значит, в каждом канале есть возможность отобразить 16 цветов. В итоге, весь RGB будет 12-битным, а отобразить он сумеет
C=16х16х16=4096 цвета
Глубина цвета в этом случае – 12 бит.
Когда говорят о 24-битном RGB, имеют в виду 8-битные каналы (по 256 цветов) с общим количеством цветовых вариантов на один пиксель
C=256x256x256=16777216 цветов.
Цифра впечатляет. Такое количество цветов для каждого пикселя удовлетворяет требованиям самого взыскательного фотохудожника.
Немного о самих форматах.
Формат TIFF
TIFF расшифровывается как «формат файла размеченного изображения» (Tagged Image File Format) и является стандартом для типографской и печатной индустрии.
В итоге, получается вот что:
1. Если ваша камера настолько проста, что снимает только JPEG, и вы хотите получить максимальное качество, задавайте максимальный размер и минимальное сжатие и не терзайте себя тем, что у вас нет других форматов. В большинстве случаев, кропотливо выведенный вручную снимок из RAW соответствует автоматически сделанному камерой JPEG.
2. Не стоит, пожалуй, фотографировать в TIFF. Запись этого формата идет тяжелее, а заметной разницы по сравнению с качественным JPEG нет.
3. Если у вас есть возможность делать снимки в , поработайте с ним. Вы сами почувствуете, подходит ли он вам. В некоторых случаях только RAW дает возможность сделать уникальное фото для большого увеличения при печати.
Остается еще одно решение, можно сказать универсальное. Есть режим, позволяющий делать кадры в двух форматах одновременно: RAW+ JPEG. Снимайте важные сюжеты в этом режиме. Современные хранилища цифровой информации – и карты памяти, и жесткие диски – позволяют это сделать. В таком случае вы получаете JPEG для использования фотографии сразу, без затрат времени на доработку. А, если понадобится этой – доверите файл RAW специалисту для обработки.
Фотография. Форматы файлов.
Легко подсчитать, что несжатое полноцветное изображение, размером 2000*1000 пикселов будет иметь размер около 6 мегабайт. Если говорить об изображениях, получаемых с профессиональных камер или сканеров высокого разрешения, то их размер может быть ещё больше. Не смотря на быстрый рост ёмкости устройств хранения, по-прежнему весьма актуальными остаются различные алгоритмы сжатия изображений.
Все существующие алгоритмы можно разделить на два больших класса:
Алгоритмы сжатия без потерь
Алгоритм RLE
Все алгоритмы серии RLE основаны на очень простой идее: повторяющиеся группы элементов заменяются на пару (количество повторов, повторяющийся элемент). Рассмотрим этот алгоритм на примере последовательности бит. В этой последовательности будут чередовать группы нулей и единиц. Причём в группах зачастую будет более одного элемента. Тогда последовательности 11111 000000 11111111 00 будет соответствовать следующий набор чисел 5 6 8 2. Эти числа обозначают количество повторений (отсчёт начинается с единиц), но эти числа тоже необходимо кодировать. Будем считать, что число повторений лежит в пределах от 0 до 7 (т.е. нам хватит 3 бит для кодирования числа повторов). Тогда рассмотренная выше последовательность кодируется следующей последовательностью чисел 5 6 7 0 1 2. Легко подсчитать, что для кодирования исходной последовательности требуется 21 бит, а в сжатом по методу RLE виде эта последовательность занимает 18 бит.Хоть этот алгоритм и очень прост, но эффективность его сравнительно низка. Более того, в некоторых случаях применение этого алгоритма приводит не к уменьшению, а к увеличению длины последовательности. Для примера рассмотрим следующую последовательность 111 0000 11111111 00. Соответствующая ей RL-последовательность выглядит так: 3 4 7 0 1 2. Длина исходной последовательности – 17 бит, длина сжатой последовательности – 18 бит.
Этот алгоритм наиболее эффективен для чёрно-белых изображений. Также он часто используется, как один из промежуточных этапов сжатия более сложных алгоритмов.
Словарные алгоритмы
Идея, лежащая в основе словарных алгоритмов, заключается в том, что происходит кодирование цепочек элементов исходной последовательности. При этом кодировании используется специальный словарь, который получается на основе исходной последовательности.Существует целое семейство словарных алгоритмов, но мы рассмотрим наиболее распространённый алгоритм LZW, названный в честь его разработчиков Лепеля, Зива и Уэлча.
Словарь в этом алгоритме представляет собой таблицу, которая заполняется цепочками кодирования по мере работы алгоритма. При декодировании сжатого кода словарь восстанавливается автоматически, поэтому нет необходимости передавать словарь вместе с сжатым кодом.
Словарь инициализируется всеми одноэлементными цепочками, т.е. первые строки словаря представляют собой алфавит, в котором мы производим кодирование. При сжатии происходит поиск наиболее длинной цепочки уже записанной в словарь. Каждый раз, когда встречается цепочка, ещё не записанная в словарь, она добавляется туда, при этом выводится сжатый код, соответствующий уже записанной в словаре цепочки. В теории на размер словаря не накладывается никаких ограничений, но на практике есть смысл этот размер ограничивать, так как со временем начинаются встречаться цепочки, которые больше в тексте не встречаются. Кроме того, при увеличении размеры таблицы вдвое мы должны выделять лишний бит для хранения сжатых кодов. Для того чтобы не допускать таких ситуаций, вводится специальный код, символизирующий инициализацию таблицы всеми одноэлементными цепочками.
Рассмотрим пример сжатия алгоритмом. Будем сжимать строку кукушкакукушонкукупилакапюшон. Предположим, что словарь будет вмещать 32 позиции, а значит, каждый его код будет занимать 5 бит. Изначально словарь заполнен следующим образом:
Эта таблица есть, как и на стороне того, кто сжимает информацию, так и на стороне того, кто распаковывает. Сейчас мы рассмотрим процесс сжатия.

В таблице представлен процесс заполнения словаря. Легко подсчитать, что полученный сжатый код занимает 105 бит, а исходный текст (при условии, что на кодирование одного символа мы тратим 4 бита) занимает 116 бит.
По сути, процесс декодирования сводится к прямой расшифровке кодов, при этом важно, чтобы таблица была инициализирована также, как и при кодировании. Теперь рассмотрим алгоритм декодирования.

Строку, добавленную в словарь на i-ом шаге мы можем полностью определить только на i+1. Очевидно, что i-ая строка должна заканчиваться на первый символ i+1 строки. Т.о. мы только что разобрались, как можно восстанавливать словарь. Некоторый интерес представляет ситуация, когда кодируется последовательность вида cScSc, где c - это один символ, а S - строка, причём слово cS уже есть в словаре. На первый взгляд может показаться, что декодер не сможет разрешить такую ситуацию, но на самом деле все строки такого типа всегда должны заканчиваться на тот же символ, на который они начинаются.
Алгоритмы статистического кодирования
Алгоритмы этой серии ставят наиболее частым элементам последовательностей наиболее короткий сжатый код. Т.е. последовательности одинаковой длины кодируются сжатыми кодами различной длины. Причём, чем чаще встречается последовательность, тем короче, соответствующий ей сжатый код.Алгоритм Хаффмана
Алгоритм Хаффмана позволяет строить префиксные коды. Можно рассматривать префиксные коды как пути на двоичном дереве: прохождение от узла к его левому сыну соответствует 0 в коде, а к правому сыну – 1. Если мы пометим листья дерева кодируемыми символами, то получим представление префиксного кода в виде двоичного дерева.Опишем алгоритм построения дерева Хаффмана и получения кодов Хаффмана.
- Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который равен частоте появления символа
- Выбираются два свободных узла дерева с наименьшими весами
- Создается их родитель с весом, равным их суммарному весу
- Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка
- Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой - бит 0
- Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Арифметическое кодирование
Алгоритмы арифметического кодирования кодируют цепочки элементов в дробь. При этом учитывается распределение частот элементов. На данный момент алгоритмы арифметического кодирования защищены патентами, поэтому мы рассмотрим только основную идею.JPEG - один из новых и достаточно мощных алгоритмов. Практически он является стандартом де-факто для полноцветных изображений . Оперирует алгоритм областями 8x8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого при разложении матрицы такой, области в двойной ряд по косинусам (см. формулы ниже) значимыми охазываютоя только первые коэффициенты..Таким образом, сжатие в JPEG осуществяяе ется за счет плавности изменения цветов в изображении.
Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битовых изображений. JPEG - Joint Photographic Expert Group- подразделение в рамках ISO - Международной организации по стандартизации. Название алгоритма читается как ["jei"peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании (в дальнейшем - ДКП), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование.
ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.
Для этого используется квантование коэффициентов (quantization). В самом простом случае- это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но может достигаться большая степень сжатия.
Как работает алгоритм
Итак, рассмотрим алгоритм подробнее (рис. 2.1). Пусть мы сжимаем 24-битовое изображение.
Шаг 1. Переводим изображение из цветового пространства RGB, с компонентами, отвечающими за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета точки, в цветовое пространство YCrCb (иногда называют YUV).
В нем Y - яркостная составляющая, а Сг, Со - компоненты, отвечающие за цвет (хроматический красный и хроматический синий). За счет того, что человеческий глаз менее чувствителен к цвету, чем к яркости, появляется возможность архивировать массивы для Сг и Со компонент с большими по терями и, соответственно, большими степенями сжатия, Подобное преобра зование уже давно используется в телевидении. На сигналы, отвечающие за цвет, там выделяется более узкая полоса частот. Упрощенно перевод из цветового пространства RGB в цветовое пространство YCrCb можно представить с помощью матрицы перехода:
Шаг 2. Разбиваем исходное изображение на матрицы 8x8. Формируем из каждой 3 рабочие матрицы ДКП - по 8 бит отдельно для каждой компоненты. При больших степенях сжатия этот шаг может выполняться чуть сложнее. Изображение делится по компоненте Y, как и в первом случае, а для компонент Сг и СЬ матрицы набираются через строчку и через столбец. То есть из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в 2 раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB-изображении, как показала практика, это сказывается несильно.
Шаг 3. В упрощенном виде ДКП при п=8 можно представить так:
nu,v] = ^Hc(i,u)xC(j,v)y r Y)
Yq
= IntegerRound На этом шаге осуществляется управление степенью сжатия и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия. С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8x8. Потери в высоких частотах могут проявиться в так называемом эффекте Гиббса,
когда вокруг контуров с резким переходом цвета образуется своеобразный "нимб". Шаг
5. Переводим матрицу 8x8 в 64-элементный вектор при помощи "зиг-заг"-сканирования, т. е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)... Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце - высоким. Шаг 6.
Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа <пропустить, число>, где "пропустить" является счетчиком пропускаемых нулей, а "число" - значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3000-2 00001 ... будет свернут в пары (0,42) (0,3) (3,-2) (4,1).... Шаг
7. Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей. Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь. Существенными положительными сторонами алгоритма является то, что: ■ задается степень сжатия; ■ выходное цветное изображение может иметь 24 бита на точку. Отрицательными сторонами алгоритма является то, что: ■ При повышении степени сжатия изображение распадается на отдельные квадраты (8x8). Это связано с тем, что происходят большие потери в низких частотах при квантовании и восстановить исходные данные становится невозможно. ■ Проявляется эффект Гиббса- ореолы по границам резких переходов цветов. Как уже говорилось, стандартизован JPEG относительно недавно -в 1991 г. Но уже тогда существовали алгоритмы, сжимающие сильнее при меньших потерях качества. Дело в том, что действия разработчиков стандарта были ограничены мощностью существовавшей на тот момент техники. То есть даже на ПК алгоритм должен был работать меньше минуты на среднем изображении, а его аппаратная реализация должна быть относительно простой и дешевой. Алгоритм должен был быть симметричным (время разархивации примерно равно времени архивации). Выполнение последнего требования сделало возможным появление таких устройств, как цифровые фотоаппараты, снимающие 24-битовые фотографии на 8-256 Мб флеш-карту." Йвтом эта карта вставляется в разъём на вашем ноутбуке и соответствующая программа позволяет считать изображения. Не правда Ня,
если бы алгоритм был несимметричен, было бы неприятно долго ждать, пока аппарат "перезарядится" - сожмет изображение. Не очень приятным свойством JPEG является также то,
что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на горизонтальные и вертикальные полосы изображения. Из-за этих сюрпризов JPEG не рекомендуется активно
использовать в полиграфии, задавая высокие коэффициенты матрицы квантования. Однако при архивации изображений, предназначенных для просмотра человеком, он на данный момент незаменим. Широкое
применение JPEG долгое время сдерживалось, пожалуй, лишь тем, что он оперирует 24-битовыми изображениями. Поэтому для того, чтобы с приемлемым качеством посмотреть картинку на обычном мониторе в 256-цветной палитре, требовалось применение соответствующих алгоритмов и, следовательно, определенное время. В приложениях, ориентированных на придирчивого пользователя, таких, например, как игры, подобные задержки неприемлемы. Кроме того, если имеющиеся у вас изображения, допустим, в 8-битовом формате GIF перевести в 24-битовый JPEG, а потом обратно в GIF для просмотра, то потеря качества произойдет дважды при обоих преобразованиях. Тем не менее выигрыш в размерах архивов зачастую настолько велик (в 3-20 раз), а потери качества настолько малы, что хранение изображений в JPEG оказывается очень эффективным. Несколько слов необходимо сказать о модификациях этого алгоритма. Хотя JPEG и является стандартом ISO, формат его файлов не был зафиксирован. Пользуясь этим, производители создают свои, несовместимые между собой форматы и, следовательно, могут изменить алгоритм. Так, внутренние таблицы алгоритма, рекомендованные ISO, заменяются ими на свои собственные. Кроме того, легкая неразбериха присутствует при задании степени потерь. Например, при тестировании выясняется, что "отличное" качество, "100%" и "10 баллов" дают существенно различающиеся картинки. При этом, кстати, "100%" качества не означает сжатия без потерь. Встречаются также варианты JPEG для специфических приложений. Как стандарт ISO JPEG начинает все шире использоваться при обмене изображениями в компьютерных сетях. Поддерживается алгоритм JPEG в форматах Quick Time, PostScript Level 2, Tiff 6.0 и на данный момент занимает видное место в системах мультимедиа. Характеристики алгоритма JPEG: o ! ш. ,. Степень сжатия:
2-200 (задается здльзователем). ,ц, :_,. . Класс изображений:
полноцветные 2jj.битовые изображения или изо-| бражения в градациях серого без резких переходов цве^о&,(фотографии). Симметричность:
1. Характерные особенности:
в некоторых случаях алгоритм создает! "ореол" вокруг резких горизонтальных и вертикальных границ в изображении (эффект Гиббса). Кроме того, при высокой степени сжатия изо-! бражение распадается на блоки 8x8 пикселов. Знание алгоритма JPEG очень полезно не только для сжатия изображений. В нем используется теория из цифровой обработки сигналов, математического анализа, линейной алгебры, теории информации, в частности, преобразование Фурье, кодирование без потерь и др. Поэтому полученные знания могут пригодиться где угодно. Если есть желание, то предлагаю пройти те же этапы самостоятельно параллельно со статьей. Проверить, насколько приведенные рассуждения подходят для разных изображений, попытаться внести свои модификации в алгоритм. Это очень интересно. В качестве инструмента могу порекомендовать замечательную связку Python + NumPy + Matplotlib + PIL(Pillow). Почти вся моя работа (в т. ч. графики и анимация), была произведена с помощью них. Внимание, трафик! Много иллюстраций, графиков и анимаций (~ 10Мб). По иронии судьбы, в статье про JPEG всего 2 изображения с этим форматом из полусотни. Будем тренироваться на кошках енотах. В качестве примера взято серое изображение, приведенное выше. Оно хорошо совмещает как однородные области, так и контрастные. А если мы научимся сжимать серое, то и с цветным не будет проблем. Можете мысленно подумать, как мог бы быть разложен сигнал, значения которого плавно уменьшаются с максимального значения в начале до минимального в конце. Более-менее адекватное приближение смогли бы сделать лишь гармоники ближе к концу, что для нас не очень здорово. На рисунке слева приближение несимметричного сигнала. Справа - симметричного: Итак, вас посетила мысль придумать свое преобразование. Помните вот что: Большие блоки не показаны, так как визуально почти неотличимы от 32x32. Теперь посмотрим на абсолютную разность с исходным изображением (усиленную в 2 раза, иначе ничего толком не видно): 8x8 дает лучший результат, чем 4x4. Дальнейшее увеличение размера уже не дает хорошо заметного преимущества. Хотя я всерьез бы задумался над 16x16, вместо 8x8: увеличение сложности на 33% (о сложности в следующем абзаце), дает небольшое, но все-таки видимое улучшение при одинаковом количестве коэффициентов. Однако, выбор 8x8 выглядит достаточно обоснованным и, возможно, является золотой серединой. JPEG был опубликован в 1991. Думаю, что такое сжатие являлось очень сложным для процессоров того времени. Второй
аргумент. Нужно помнить, что при увеличении размера блока потребуется больше вычислений. Давайте оценим насколько. Сложность преобразования в лоб, как мы уже вполне умеем: O(N 2), так как каждый коэффициент состоит из N слагаемых. Но на практике используется эффективный алгоритм быстрого преобразования Фурье (БПФ, Fast Fourier Transform, FFT). Его описание выходит за рамки статьи. Его сложность: O(N*logN). Для двумерного разложения нужно воспользоваться им дважды по N раз. Таким образом, сложность 2D DCT - O(N 2 logN). Теперь сравним сложности вычисления изображения одним блоком и несколькими маленькими: Третий
аргумент. Если у нас на изображении есть резкая граница цветов, то это скажется на всем блоке. Возможно, лучше этот блок будет достаточно мал, ведь во многих соседних блоках, такой границы, вероятно, уже не будет. Однако, вдали от границ затухание происходит достаточно быстро. К тому же сама граница будет выглядеть лучше. Проверим на примере с большим количеством контрастных переходов, опять же, только с четвертью коэффициентов: И на десерт, рассмотрим качество 5% (при кодировании в Fast Stone). Кстати, насчет 100% качества. Как вы догадываетесь, в этом случае матрица квантования состоит полностью из единиц, то есть квантования не происходит. Однако, из-за округления коэффициентов до целого, мы не можем в точности восстановить исходную картинку. Например, енот сохранил 96% пикселей точно, а 4% отличались на 1/256. Разумеется, такие «искажения» невозможно заметить визуально. Пример 0
(для разминки) Подобные слова мы будем обозначать как A, B, C..., и называть их символами. Причем под символом может скрываться что угодно: буква алфавита, слово или бегемот в зоопарке. Главное, что одинаковым символам соответствуют одинаковые понятия, а разным - разные. Так как наша задача - эффективное кодирование (сжатие), то будем работать с битами, так как это наименьшие единицы представления информации. Поэтому, запишем список как ABBAAABA. Вместо «первое слово» и «второе слово» можно использовать биты 0 и 1. Тогда ABBAAABA закодируется как 01100010 (8 бит = 1 байт). Пример 1
Пример 2
Пример 3
Пример 4
Теперь порядок. Мы разобрались как хранятся DC: Смотрим AC: Строим гистограмму зависимости количества по этим парам и дерево Хаффмана. Особенности реализации в JPEG:
Выяснили, что каждый блок закодирован хранится в файле так: Я надеюсь, что теперь вам понятен алгоритм JPEG интуитивно. Спасибо за прочтение! UPD
Теги:
Добавить метки Для эффективного сжатия данных необходимо прежде всего оценить характер вашего изображения. JPEG сжимает графические данные, опираясь на то, что видит человеческий глаз. Поэтому, чтобы помочь понять, как и что делает JPEG, я хотел бы дать вам общее представление о зрительном восприятии человека. Сжатие JPEG происходит в несколько этапов. Цель - преобразовать графические данные таким образом, чтобы незначимая визуальная информация легко идентифицировалась и отбрасывалась. Такое сжатие "с потерями" отличается от большинства других подходов, используемых при работе с графическими форматами, которые стараются сохранить в неприкосновенности каждый бит изображения. Цветовая модель
Первый шаг JPEG - выбор подходящего способа представления цветов. Цвета обычно задаются в трехмерной системе координат. Хорошо известная большинству программистов система описывает цвет, как комбинацию красного, зеленого и синего (RGB). К несчастью, с точки зрения возможности сжатия, это не лучший способ описания цвета. Проблема заключается в том, что все три компонента: красный, зеленый и синий - равнозначны. Однако переход к другой системе цветопередачи позволяет выделить некоторую более важную информацию. Профессионалы используют две цветовые модели: HSL (Hue-Saturation-Lightness) и HSV (Hue-Saturation-Value). Интуитивно понятно, что яркостная компонента (Lightness) модели HSL и яркостная компонента (Value) модели HSV каждая по-своему определяют соотношение света и тени. Насыщенность (saturation) определяет уровень "чистого" цвета. Ненасыщенные цвета часто неформально называют "грязными" (greyish). Оттенок (Hue) - это то, что мы воспринимаем, как цвет предмета, например красный или серовато-зеленый. Здесь важно отметить удивительный факт: человеческое зрение более чувствительно к изменению освещенности, а не цвета как такового! Различные реализации алгоритма сжатия JPEG используют различные цветовые системы. Используемая форматом JFIF система цветопередачи YCbCr во многом схожа со схемой, разработанной много лет назад для цветного телевидения. Прореживание
Основная причина преобразования одной цветовой модели в другую заключается в необходимости выявления менее существенной для просмотра информации изображения. JPEG уменьшает количество информации о цвете. В то время как яркостная компонента передается с полным разрешением, цветоразностностные компоненты используют в два раза меньший диапазон значений. В результате этого простого шага объем данных уменьшается на треть. С помощью прореживания (subsampling) регулируются цвета изображения цветного телевизора. Обычно в телевидение черно-белое изображение и информация о цвете передаются по отдельности. Причем информация о цвете передается в менее строгом виде, чем информация о яркости изображения. Дискретное косинусное преобразование (DCT)
Каждая компонента цвета обрабатывается отдельно, как если бы они были не одним цветным, а тремя полутоновыми изображениями. Если вы посмотрите на детальное изображение с большого расстояния, то вы различите лишь общий тон картины. Например, "главным образом синий" или "преимущественно красный". Чем ближе вы будете подходить к изображению, тем больше деталей сможете различить. Для эмуляции этого эффекта JPEG использует один математический прием, называемый дискретным косинусным преобразованием (DCT). DCT преобразует информацию о пикселах в информацию об изменении пикселов. Первое, что может дать DCT - усредненный цвет области. Затем он все больше и больше уточняет детали. Как в случае удаленного изображения, усредненное значение цвета представляет собой очень важную информацию об области изображения. Ваш глаз менее чувствителен к скорости изменения цвета, поэтому она не так важна. Преобразовав информацию о цвете подобным образом, мы выделяем ту информацию, которой можно пожертвовать. Считается, что потери обусловливаются именно этим этапом. Если вы с помощью DCT закодируете изображение и затем с помощью функции обратного DCT восстановите его, то вы не получите абсолютно такой же набор бит. Однако эта ошибка - ошибка округления. Она возникает при выполнении арифметических действий и обычно не очень велика. Поэтому я предпочитаю думать об этапе DCT, как о действии, происходящем "в основном без потерь". Для больших изображений обсчет DCT и обратного DCT весьма времяемкий процесс. Чтобы сократить время расчетов, JPEG разбивает изображение на мозаику размером восемь на восемь пикселов. Каждая из мозаик обрабатывается отдельно, что существенно сокращает необходимое для DCT время расчета. Проблема, возникающая при таком подходе, состоит в том, что после квантования (о котором пойдет речь в следующем разделе) границы этих квадратиков могут не совпадать и потому становятся видимыми при задании низкого значения параметра качества. Квантование
Разработчиков JPEG прежде всего интересовали изображения фотографического качества (photographic, contnuous tone). Как правило, эти полутоновые изображения характеризуются мягкими переходами от одного цвета к другому. Для таких изображений низкочастотная (медленно изменяющаяся) компонента DCT важнее высокочастотной (быстро меняющаяся). Термин квантование (quantization) означает просто "округление". JPEG отбрасывает некоторую графическую информацию за счет округления каждого члена DCT с различными весовыми коэффициентами, опираясь при этом на различные факторы. Высокочастотная компонента округляется сильнее низкочастотной. Например, низкочастотная компонента, которая хранит среднюю величину яркости, может быть округлена до значения, кратного трем, в то время как высокочастотная компонента может быть округлена до значения, кратного ста! Операция квантования объясняет, почему сжатие JPEG в случае четких контуров приводит к образованию "дрожащих" линий. Контуры определяются высокочастотной (быстро меняющейся) пространственной компонентой. (На первый взгляд может показаться, что вы должны получить размытый контур, однако вспомните, что C в сокращении DCT обозначает косинус.) Обычно цветовые плоскости квантуются гораздо грубее плоскостей яркости. Здесь правильный выбор цветовой модели помогает выявлять ту информацию, которую можно отбросить. Сжатие
До сих пор, за исключением того случая, когда рассматривалась частота выборки из двух цветовых каналов, никакого сжатия не происходило. Все рассмотренные выше шаги - преобразование цветовых моделей, DCT и квантование - оставляли размер данных без изменений. Наконец мы добрались до последнего шага, во время которого с помощью стандартной техники сжатия без потерь действительно будет уменьшен размер данных. Данные, разложенные по полочкам в ходе предыдущих шагов, могут быть сжаты более эффективно, чем необработанное сырье, которое представляют собой графические данные RGB. Причем ни один из сделанных шагов не был лишним, каждое изменение данных было направлено на то, чтобы более эффективно сжать окончательный вариант. Изменение цветовой модели позволило проредить информацию каналов и затем более энергично их квантовать. DCT дало возможность выделить высокочастотную пространственную компоненту. Высокочастотная компонента обычно имеет небольшие значения, в результате чего выходные данные на этапе DCT содержат несоразмерно много маленьких значений, облегчающих процесс сжатия. В процессе квантования большая часть высокочастотной составляющей обнуляется, а остальная принимает конкретные значения. Сокращение числа различных значений также облегчает процесс сжатия данных. Стандарт JPEG предоставляет два различных метода сжатия без потерь, которые могут быть использованы на последнем этапе. Сжатие Хаффмана (Huffman compression - это давно известный незапатентованный, легко программируемый алгоритм. В отличие от него более новый алгоритм арифметического кодирования (arithmetic coding) является объектом многочисленных патентов. (Поэтому не удивительно, что многие программы сжатия JPEG поддерживают только сжатие Хаффмана.) При декодировании изображений JPEG необходимо совершить все эти шаги в обратном порядке. Поток данных вначале распаковывается, затем каждый блок 8ґ8 подвергается обратному DCT и наконец изображение конвертируется в соответствующую цветовую модель (обычно это RGB). Отметим, что информация, которая была обдуманно отброшена с помощью прореживания и квантования, никогда не восстанавливается. Однако если все было сделано корректно, потеря информации не вызовет никакого видимого ухудшения изображения. Алгоритм преобразования графического изображения JPEG состоит из нескольких этапов, выполняемых над изображением последовательно, один за другим: – преобразования цветового пространства, – субдискретизации, – дискретного косинусного преобразования (ДКП), – квантования, – кодирования. На этапе преобразования цветового пространства осуществляется преобразование изображения из цветового пространства RGB в YCbCr (где Y - яркость, а Cb и Cr - цветоразностные компоненты точки изображения): Применение пространства YCbCr
вместо привычного RGB
объясняется физиологическими особенностями человеческого зрения, а именно тем, что нервная система человека обладает значительно большей чувствительностью к яркости (Y
) , чем к цветоразностным составляющим (в данном случае Cb
и Cr
). Обратное преобразование цветового пространства (из YCrCb
в RGB
) имеет вид: Алгоритм сжатия JPEG позволяет сжимать изображения с различными размерами цветовых плоскостей. Обозначим через x i
и y i
ширину и высоту i
-й цветовой плоскости изображения. Пусть X
= max
(x i
), Y
= max
(y i
), определим для каждой плоскости коэффициенты H i
= X
/ x i
и V i
= Y
/ y i
. Наибольшее значение для X
и Y
согласно алгоритму JPEGравно 2 16 , а для H i
и V i
– 2 2 . Таким образом, ширина и высота цветовых плоскостей может быть от 1 до 4 раз меньше, размеров наибольшей плоскости. Для обычных RGB
изображений размеры всех цветовых плоскостей равны. Субдискретизация состоит в уменьшении размеров плоскостей Cr
и Cb
. Наиболее распространено уменьшение в 2 раза по ширине и в 2 раза по высоте (см. рисунок 1). Для этого Cr
и Cb
плоскости изображения разбиваются на блоки с размером 2 на 2 точки, и блок заменяется одним отсчетом цветоразностных компонент (на место имевшихся 4 отсчетов ставится их среднее арифметическое для каждого блока, что позволяет уменьшить размер исходного изображения в 2 раза). Рисунок 1 – Распространенные типы субдискретизации Затем, отдельно для каждого компонента цветового пространства Y
, Cb
и Cr
, осуществляется прямое дискретное косинусное преобразование. Для этого изображение делится на блоки с размером 8 на 8 точек и каждый блок преобразуется согласно формуле: Применение дискретного косинусного преобразования позволяет перейти от пространственного представления изображения к спектральному. Обратное дискретное косинусное преобразование имеет вид: После этого можно переходить к квантованию полученной информации. Идея квантования состоит в отбрасывании некоторого объема информации. Известно, что глаз человека менее восприимчив к высоким частотам (особенно к высоким частотам цветоразностных компонент), большинство фотографических изображений содержит мало высокочастотных составляющих. Кроме того, появление высоких частот является следствием процесса оцифровки, т.е. вследствие появления сопутствующих дискретизации и квантования шумов. На этом этапе используются так называемые таблицы квантования
- матрицы состоящие из целых положительных чисел с размером 8 на 8, на элементы которых делятся соответствующие частоты блоков изображения, результат округляется до целого числа: В процессе деквантования используются те же таблицы, что и при квантовании. Деквантование состоит в умножении квантованных частот на соответствующие элементы таблицы квантования: Таким образом, при увеличении коэффициента квантования увеличивается объем отбрасываемой информации. Рассмотрим это подробнее на примере. Блок до квантования: 3862, –22, –162, –111, –414, 12, 717, 490, 383, 902, 913, 234, –555, 18, –189, 236, 229, 707, –708, 775, 423, –411, –66, –685, 231, 34, –928, 34, –1221, 647, 98, –824, –394, 128, –307, 757, 10, –21, 431, 427, 324, –874, –367, –103, –308, 74, –1017, 1502, 208, –90, 114, –363, 478, 330, 52, 558, 577, 1094, 62, 19, –810, –157, –979, –98 Таблица квантования (качество 90): 24, 16, 16, 24, 40, 64, 80, 96, 16, 16, 24, 32, 40, 96, 96, 88, 24, 24, 24, 40, 64, 88, 112, 88, 24, 24, 32, 48, 80, 136, 128, 96, 32, 32, 56, 88, 112, 176, 168, 120, 40, 56, 88, 104, 128, 168, 184, 144, 80, 104, 128, 136, 168, 192, 192, 160, 112, 144, 152, 160, 176, 160, 168, 160 Блок после квантования: 161, –1, –10, –5, –10, 0, 9, 5, 24, 56, 38, 7, –14, 0, –2, 3, 10, 29, –30, 19, 7, –5, –1, –8, 10, 1, –29, 1, –15, 5, 1, –9, –12, 4, –5, 9, 0, 0, 3, 4, 8, –16, –4, –1, –2, 0, –6, 10, 3, –1, 1, –3, 3, 2, 0, 3, 5, 8, 0, 0, –5, –1, –6, –1 3864, –16, –160, –120, –400, 0, 720, 480, 384, 896, 912, 224, –560, 0, –192, 264, 240, 696, –720, 760, 448, –440, –112, –704, 240, 24, –928, 48,–1200, 680, 128, –864, –384, 128, –280, 792, 0, 0, 504, 480, 320, –896, –352, –104, –256, 0,–1104, 1440, 240, –104, 128, –408, 504, 384, 0, 480, 560, 1152, 0, 0, –880, –160,–1008, –160 Таблица квантования (качество 45): 144, 96, 88, 144, 216, 352, 456, 544, 104, 104, 128, 168, 232, 512, 536, 488, 128, 112, 144, 216, 352, 504, 616, 496, 128, 152, 192, 256, 456, 776, 712, 552, 160, 192, 328, 496, 600, 968, 912, 680, 216, 312, 488, 568, 720, 920, 1000, 816, 432, 568, 696, 776, 912, 1072, 1064, 896, 640, 816, 840, 872, 992, 888, 912, 880 Блок после квантования: 27, 0, –2, –1, –2, 0, 2, 1, 4, 9, 7, 1, –2, 0, 0, 0, 2, 6, –5, 4, 1, –1, 0, –1, 2, 0, –5, 0, –3, 1, 0, –1, –2, 1, –1, 2, 0, 0, 0, 1, 2, –3, –1, 0, 0, 0, –1, 2, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, –1, 0, –1, 0 Блок после обратного преобразования: 3888, 0, –176, –144, –432, 0, 912, 544, 416, 936, 896, 168, –464, 0, 0, 0, 256, 672, –720, 864, 352, –504, 0, –496, 256, 0, –960, 0,–1368, 776, 0, –552, –320, 192, –328, 992, 0, 0, 0, 680, 432, –936, –488, 0, 0, 0,–1000, 1632, 0, 0, 0, 0, 912, 0, 0, 896, 640, 816, 0, 0, –992, 0, –912, 0 Как видно, в первом случае изменение DC
коэффициента в результате сжатия равно 2, а во втором 26, при этом квантованный DC
коэффициент во втором случае в 6 раз меньше чем в первом. Кодирование является заключительным этапом сжатия, во время него блоки изображения преобразуются в векторную форму по правилу, задаваемому блоками вида: 0, 1, 5, 6, 14, 15, 27, 28, 2, 4, 7, 13, 16, 26, 29, 42, 3, 8, 12, 17, 25, 30, 41, 43, 9, 11, 18, 24, 31, 40, 44, 53, 10, 19, 23, 32, 39, 45, 52, 54, 20, 22, 33, 38, 46, 51, 55, 60, 21, 34, 37, 47, 50, 56, 59, 61, 35, 36, 48, 49, 57, 58, 62, 63 где в качестве элементов блока указаны векторные индексы соответствующих компонентов матрицы. При этом нулевой элемент кодируется как разница с нулевым элементом предыдущего блока. Нулевые элементы обозначают DC
, в них содержится постоянная составляющая блока (все остальные АС элементы принято обозначать AC
). Затем полученные данные сжимаются с использованием арифметического кодирования или модификации алгоритма Хаффмана. Этот этап не представляет большого интереса с точки зрения стеганографии в графических изображениях, поэтому он выходит за рамки нашего рассмотрения.
Вы правильно поняли из названия, что это не совсем обычное описание алгоритма JPEG (формат файла я подробно описывал в статье «Декодирование JPEG для чайников»). В первую очередь, выбранный способ подачи материала предполагает, что мы ничего не знаем не только о JPEG, но и о преобразовании Фурье, и кодировании Хаффмана. И вообще, мало что помним из лекций. Просто взяли картинку и стали думать как же ее можно сжать. Поэтому я попытался доступно выразить только суть, но при которой у читателя будет выработано достаточно глубокое и, главное, интуитивное понимание алгоритма. Формулы и математические выкладки - по самому минимуму, только те, которые важны для понимания происходящего.
Каков бы ни был алгоритм сжатия информации, его принцип всегда будет один - нахождение и описание закономерностей. Чем больше закономерностей, тем больше избыточности, тем меньше информации. Архиваторы и кодеры обычно «заточены» под конкретный тип информации, и знают где можно их найти. В некоторых случаях закономерность видна сразу, например картина голубого неба. Каждый ряд его цифрового представления можно довольно точно описать прямой. Векторное представление
Для начала проверим насколько зависимы два соседних пикселя. Логично предположить, что скорее всего, они будут очень похожи. Проверим это для всех пар изображения. Отметим их на координатной плоскости точками так, что значение точки по оси X - значение первого пикселя, по оси Y - второго. Для нашего изображения размером 256 на 256 получим 256*256/2 точек:
Предсказуемо, что большинство точек находится на или рядом с прямой y=x (а их там еще больше, чем видно на рисунке, так как они многократно накладываются друг на друга, и, к тому же, они полупрозрачные). А раз так, то было бы проще работать, повернув их на 45°. Для этого нужно выразить их в другой системе координат.
Базисные вектора новой системы, очевидно, такие: . Вынуждены делить на корень из двойки, чтобы получить ортонормированную систему (длины базисных векторов равны единичке). Здесь показано, что некоторая точка p = (x, y) в новой системе будет представлена как точка (a 0 , a 1). Зная новые коэффициенты, мы легко можем получить старые обратным поворотом. Очевидно, первая (новая) координата является средним, а вторая - разностью x и y (но деленные на корень из 2). Представьте, что вам предложено оставить только одно из значений: либо a 0 , либо a 1 (то есть другое приравнять нулю). Лучше выбрать a 0 , так как значение a 1 и так, скорее всего, будет около нуля. Вот, что получится, если мы восстановим изображение только по a 0:
Увеличение в 4 раза:
Такое сжатие не очень впечатляет, честно говоря. Лучше аналогично разобьем картинку по тройкам пикселей и представим их в трехмерном пространстве.

Это один и тот же график, но с разных точек зрения. Красные линии - оси, которые напрашивались сами собой. Им соответствуют вектора: . Напоминаю, что приходится делить на некоторые константы, чтобы длины векторов стали равны единице. Таким образом, разложив по такому базису, мы получим 3 значения a 0 , a 1 , a 2 , причем a 0 важнее a 1 , а a 1 важнее a 2 . Если мы выбросим a 2 , то график «сплющится» в направлении вектора e 2 . Этот и так довольно не толстый трехмерный лист станет плоским. Он потеряет не так много, зато мы избавимся от трети значений. Сравним изображения, восстановленные по тройкам: (a 0 , 0, 0), (a 1 , a 2 , 0) и (a 0 , a 1 , a 2). В последнем варианте мы ничего не выбросили, поэтому получим оригинал.
Увеличение в 4 раза:
Второй рисунок уже хорош. Резкие участки немного сгладились, но в целом картинка сохранилась очень неплохо. А теперь, точно так же поделим на четверки и визуально определим базис в четырехмерном пространстве… А, ну да. Но можно догадаться, каким будет один из векторов базиса, это: (1,1,1,1)/2. Поэтому можно посмотреть проекцию четырехмерного пространства на пространство, перпендикулярное вектору (1,1,1,1), чтобы выявить другие. Но это не лучший путь.
Наша цель - научиться преобразовывать (x 0 , x 1 , ..., x n-1) к (a 0 , a 1 , ..., a n-1) так, что каждое значение a i все менее важно, чем предыдущие. Если мы сможем так делать, то, возможно, последние значения последовательности вообще можно будет выбросить. Вышеприведенные опыты намекают, что можно. Но без математического аппарата не обойтись.
Итак, нужно преобразовать точки к новому базису. Но сначала необходимо найти подходящий базис. Вернемся к первому эксперименту разбиения на пары. Будем считать обобщенно. Мы определили базисные векторы:
Выразили через них вектор p
:
или в координатах:
Чтобы найти a 0 и a 1 нужно спроецировать p
на e
0 и e
1 соответственно. А для этого нужно найти скалярное произведение
аналогично:
В координатах:
Часто бывает удобнее проводить преобразование в матричной форме. 
Тогда A = EX и X = E T A. Это красивая и удобная форма. Матрица E называется матрицей преобразования и является ортогональной, с ней мы еще встретимся. Переход от векторов к функциям.
С векторами малых размерностей работать удобно. Однако мы хотим находить закономерности в бОльших блоках, поэтому вместо N-мерных векторов удобнее оперировать последовательностями, которыми представлено изображение. Такие последовательности я буду называть дискретными функциями, так как следующие рассуждения применимы и к непрерывным функциям.
Возвращаясь к нашему примеру, представим такую функцию f(i), которая определена всего в двух точках: f(0)=x и f(1)=y. Аналогично зададим базисные функции e 0 (i) и e 1 (i) на основе базисов e
0 и e
1 . Получим:
Это очень важный вывод. Теперь во фразе «разложение вектора по ортонормированным векторам» мы можем заменить слово «вектор» на «функция» и получить вполне корректное выражение «разложение функции по ортонормированным функциям». Не беда, что мы получили такую куцую функцию, так как такие же рассуждения работают и для N-мерного вектора, который можно представить как дискретную функцию с N значениями. А работа с функциями нагляднее, чем с N-мерными векторами. Можно и наоборот, представить такую функцию как вектор. Более того, обычную непрерывную функцию можно представить бесконечномерным вектором, правда уже не в евклидовом, а гильбертовом пространстве. Но мы туда не пойдем, нас будут интересовать только дискретные функции.
А наша задача нахождения базиса превращается в задачу нахождения подходящей системы ортонормированных функций. В следующих рассуждениях предполагается, что мы уже как-то определили набор базисных функций, по которым и будем раскладывать.
Допустим, у нас есть некоторая функция (представленная, например, значениями), которую мы хотим представить в виде суммы других. Можно представлять этот процесс в векторном виде. Для разложения функции нужно «спроецировать» ее на базисные функции по очереди. В векторном смысле вычисление проекции дает минимальное сближение исходного вектора к другому по расстоянию. Помня о том, что расстояние вычисляется с помощью теоремы Пифагора, то аналогичное представление в виде функций дает наилучшее среднеквадратичное приближение функции к другой. Таким образом, каждый коэффициент (k) определяет «близость» функции. Более формально, k*e(x) - лучшее среднеквадратичное приближение к f(x) среди l*e(x).
В следующем примере показан процесс приближения функции только по двум точкам. Справа - векторное представление.
Применительно к нашему эксперименту разбивания на пары, можно сказать, что эти две точки (0 и 1 по абсцисс) - пара соседних пикселей (x, y).
То же самое, но с анимацией:
Если мы возьмем 3 точки, то нужно рассматривать трехмерные вектора, однако приближение будет точнее. А для дискретной функции с N значениями нужно рассматривать N-мерные вектора.
Имея набор полученных коэффициентов, можно легко получить исходную функцию, просуммировав базисные функции, взятые с соответствующими коэффициентами. Анализ этих коэффициентов может дать много полезной информации (в зависимости от базиса). Частным случаем этих соображений является принцип разложения в ряд Фурье. Ведь наши рассуждения применимы к любому базису, а при разложении в ряд Фурье берется вполне конкретный.Дискретные преобразования Фурье (ДПФ)
В предыдущей части мы пришли к выводу, что неплохо было бы разлагать функцию на составные. В начале 19 века Фурье тоже задумался над этим. Правда картинки с енотом у него не было, поэтому ему пришлось исследовать распределение тепла по металлическому кольцу. Тогда он выяснил, что очень удобно выражать температуру (и ее изменение) в каждой точке кольца как сумму синусоид с разными периодами. «Фурье установил (рекомендую к прочтению , интересно), что вторая гармоника затухает в 4 раза быстрее, чем первая, а гармоники более высоких порядков затухают с ещё большей скоростью».
В общем, вскоре оказалось, что периодичные функции замечательно раскладываются на сумму синусоид. А так как в природе существует много объектов и процессов, описывающимися периодичными функциями, то появился мощный инструмент их анализа.
Пожалуй, один из самых наглядных периодических процессов - это звук.
Если бы мне дали значения последней функции на тот момент, когда я не знал про ряды Фурье, и попросили проанализировать их, то я бы точно растерялся и не смог бы сказать ничего путного. Ну, да, какая-то функция, но как понять, что там есть что-то упорядоченное? Но если бы я догадался прослушать последнюю функцию, то ухо уловило бы чистый тон среди шума. Хотя и не очень хорошо, так как я специально при генерации подобрал такие параметры, чтобы на суммарном графике сигнал визуально растворился в шуме. Как я понял, до сих пор точно не уставлено, как слуховой аппарат делает это. Однако, недавно стало ясно, что он не раскладывает звук на синусоиды. Возможно, когда-нибудь мы поймем как это происходит, и появятся более совершенные алгоритмы. Ну, а мы пока по старинке.
Почему бы не попробовать взять синусоиды в качестве базиса? На самом деле мы фактически уже сделали это. Вспомним наше разложение на 3 базисных вектора и представим их на графике:
Да-да, знаю, это выглядит как подгонка, но с тремя векторами трудно ожидать большего. Зато теперь понятно, как получить, например, 8 базисных векторов:
Не очень сложная проверка показывает, что эти вектора попарно перпендикулярны, т. е. ортогональны. Это значит, их можно использовать как базис. Преобразование по такому базису широко известно, и называется дискретным косинусным преобразованием (DCT). Думаю, из приведенных графиков понятно как получается формула DCT-преобразования:
Это все та же формула: A = EX с подставленным базисом. Базисные вектора указанного DCT (они же векторы-строки матрицы E) ортогональны, но не ортонормированы. Это следует помнить при обратном преобразовании (не буду останавливаться на этом, но, кому интересно - у inverse DCT появляется слагаемое 0.5*a 0 , так как нулевой вектор базиса больше остальных).
На следующем примере показан процесс приближения промежуточных сумм к исходным значениям. На каждой итерации очередной базис умножается на очередной коэффициент и прибавляется к промежуточной сумме (то есть так же, как и в ранних опытах над енотом - треть значений, две трети). 
Но, все-таки, несмотря на некоторые доводы о целесообразности выбора такого базиса, реальных аргументов пока нет. Действительно, в отличие от звука, целесообразность разложения изображения на периодические функции гораздо менее очевидна. Впрочем, изображение действительно может быть слишком непредсказуемым даже на небольшом участке. Поэтому, картинку делят на достаточно маленькие кусочки, но не совсем крохотные, чтобы разложение имело смысл. В JPEG изображение «нарезается» на квадраты 8x8. В пределах такого кусочка фотографии обычно очень однородны: фон плюс небольшие колебания. Такие области шикарно приближаются синусоидами.
Ну, допустим, этот факт более или менее понятен интуитивно. Но появляется нехорошее предчувствие насчет резких цветовых переходов, ведь медленно изменяющиеся функции нас не спасут. Приходится добавлять разные высокочастотные функции, которые справляются со своей работой, но побочно проявляются на однородном фоне. Возьмем изображение 256x256 с двумя контрастными областями:
Разложим каждую строку с помощью DCT, получив, таким образом, по 256 коэффициентов на строку.
Затем оставим только первые n коэффициентов, а остальные приравняем нулю, и, поэтому, изображение будет представлено в виде суммы только первых гармоник:
Число на картинке - количество оставленных коэффициентов. На первом изображении осталось только среднее значение. На второй уже добавилась одна низкочастотная синусоида, и т. д. Кстати, обратите внимание на границу - несмотря на все лучшее приближение, рядом с диагональю хорошо заметны 2 полоски, одна светлее, другая темнее. Часть последнего изображения увеличенного в 4 раза:
И вообще, если вдали от границы мы видим первоначальный равномерный фон, то при приближении к ней, амплитуда начинает расти, наконец достигает минимального значения, а затем резко становится максимальным. Это явление известно как эффект Гиббса.
Высота этих горбов, появляющийся около разрывов функции, не уменьшится при увеличении количества слагаемых функций. В дискретном преобразовании оно пропадает только при сохранении почти всех коэффициентов. Точнее, становится незаметным.
Следующий пример полностью аналогичен вышеприведенному разложению треугольников, но уже на реальном еноте:
При изучении DCT может сложиться ложное впечатление, что всегда вполне достаточно всего нескольких первых (низкочастотных) коэффициентов. Это верно для многих кусочков фотографий, тех, чьи значения не меняются резко. Однако, на границе контрастных участков значения будут резво «скакать» и даже последние коэффициенты будут велики. Поэтому, когда слышите о свойстве сохранения энергии DCT, делайте поправку на то, что оно относится ко многим видам встречаемых сигналов, но не ко всем. Для примера подумайте, как будет выглядеть дискретная функция, коэффициенты разложения которой равны нулю, кроме последнего. Подсказка: представьте разложение в векторном виде.
Несмотря на недостатки, выбранный базис является одним из лучших на реальных фотографиях. Чуть позже мы увидим небольшое сравнение с другими.DCT vs все остальное
Когда я изучал вопрос ортогональных преобразований, то, честно говоря, меня не очень убеждали доводы о том, что все вокруг - это сумма гармонических колебаний, поэтому нужно и картинки раскладывать на синусоиды. А может быть лучше подойдут какие-нибудь ступенчатые функции? Поэтому искал результаты исследований об оптимальности DCT на реальных изображениях. То, что «Именно DCT чаще всего встречается в практических приложениях благодаря свойству «уплотнения энергии»» написано везде. Это свойство означает, что максимальное количество информации заключено в первых коэффициентах. А почему? Нетрудно провести исследование: вооружаемся кучей разных картинок, различными известными базисами и начинаем считать среднеквадратичное отклонение от реального изображения для разного количества коэффициентов. Нашел небольшое исследование в статье (использованные изображения ) по этой методике. В ней приведены графики зависимости сохраненной энергии от количества первых коэффициентов разложений по разным базисам. Если вы просмотрели графики, то убедились, что DCT стабильно занимает почетное… эмм… 3-место. Как же так? Что еще за KLT преобразование? Я восхвалял DCT, а тут…KLT
Все преобразования, кроме KLT, являются преобразованиями с постоянным базисом. А в KLT (преобразование Карунена-Лоэва) вычисляется самый оптимальный базис для нескольких векторов. Он вычисляется таким образом, что первые коэффициенты дадут наименьшую среднеквадратичную погрешность суммарно для всех векторов. Похожую работу мы проводили ранее вручную, визуально определяя базис. Сначала кажется, что это здравая идея. Мы могли бы, например, разбивать изображение на небольшие секции и для каждой вычислять свой базис. Но мало того, что появляется забота хранения этого базиса, так еще и операция его вычисления достаточно трудоемкая. А DCT проигрывает лишь немного, и к тому же у DCT существуют алгоритмы быстрого преобразования.DFT
DFT (Discrete Fourier Transform) - дискретное преобразование Фурье. Под этим названием иногда упоминается не только конкретная трансформация, но и весь класс дискретных трансформаций (DCT, DST...). Посмотрим на формулу DFT:
Как вы догадываетесь, это ортогональное преобразование с каким-то комплексным базисом. Так как подобная комплексная форма встречается чуть чаще, чем всегда, то имеет смысл изучить ее вывод.
Может сложится впечатление, что любой чистый гармонический сигнал (с целой частотой) при DCT разложении будет давать только один ненулевой коэффициент, соответствующий этой гармонике. Это не так, поскольку помимо частоты, важна и фаза этого сигнала. Например, разложение синуса по косинусам (подобным образом и в дискретном разложении) будет таким:
Вот вам и чистая гармоника. Она наплодила кучу других. На анимации показаны коэффициенты DCT синусоиды в разных фазах.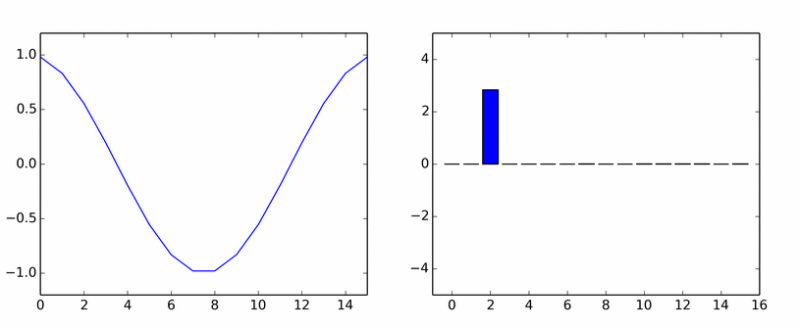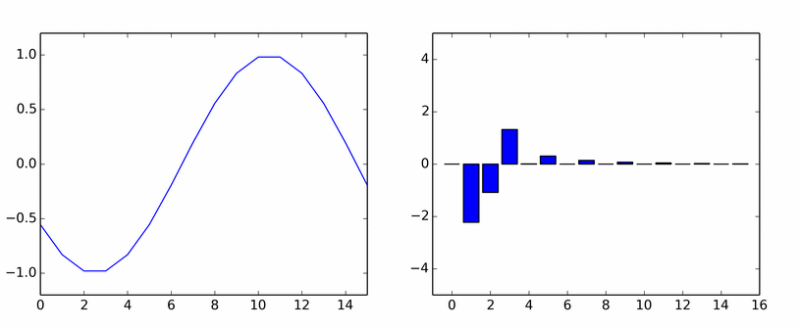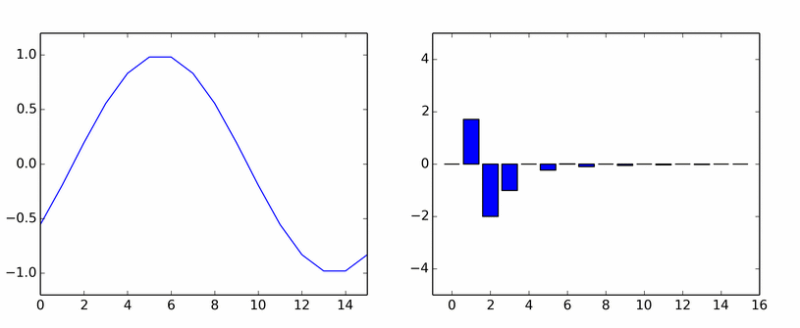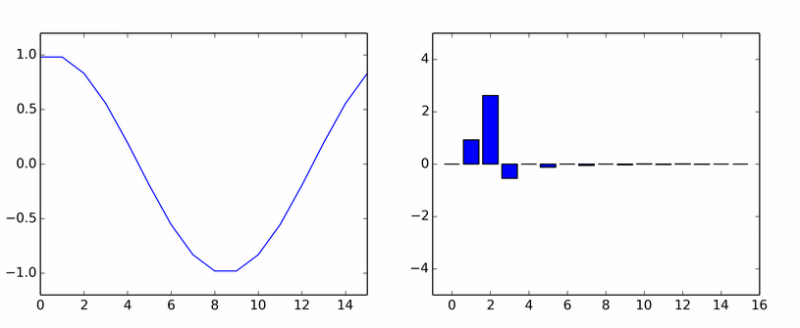
Если вам показалось, что столбики вращаются вокруг оси, то вам не показалось.
Значит теперь будем раскладывать функцию на сумму синусоид не просто разных частот, но еще и смещенных по какой-то фазе. Будет удобнее рассмотреть сдвиг фаз на примере косинуса:
Простое тригонометрическое тождество дает важный результат: сдвиг по фазе заменяется суммой синуса и косинуса, взятых с коэффициентами cos(b) и sin(b). Значит, можно раскладывать функции на сумму синусов и косинусов (без всяких фаз). Это распространенная тригонометрическая форма. Однако, гораздо чаще используется комплексная. Для ее получения нужно воспользоваться формулой Эйлера . Просто подставим производные формулы для синуса и косинуса, получим:
Теперь небольшая замена. Верхнее подчеркивание - сопряженное число.
Получим итоговое равенство:
c - комплексный коэффициент, действительная часть которого равна косинусному коэффициенту, а мнимая - синусному. А множество точек (cos(b), sin(b)) является окружностью. В такой записи каждая гармоника входит в разложение и с положительной и с отрицательной частотой. Поэтому в различных формулах Фурье-анализа обычно происходит суммирование или интегрирование от минус до плюс бесконечности. Производить вычисления часто бывает удобнее именно в такой комплексной форме.
Преобразование раскладывает сигнал на гармоники с частотами от одного до N колебаний на области сигнала. Но частота дискретизации составляет N на области сигнала. А по теореме Котельникова (aka теорема Найквиста - Шеннона) частота дискретизации должна по крайней мере в два раза превышать частоту сигнала. Если это не так, то получается эффект появления сигнала с ложной частотой:
Пунктирной линий показан неверно восстановленный сигнал. С таким явлением вы часто сталкивались в жизни. Например, забавное движение колес автомобиля на видео, или муаровый эффект.
Это приводит к тому, что вторая половина из N комплексных амплитуд как будто состоит из других частот. Эти ложные гармоники второй половины являются зеркальным отображением первой и не несут дополнительной информации. Таким образом, у нас остается N/2 косинусов и N/2 синусов (образующих ортогональный базис).
Ладно, базис есть. Его составляющие - гармоники с целым числом колебаний на области сигнала, а значит, крайние значения гармоник равны. Точнее почти равны, так как последнее значение берется не совсем с края. Более того - каждая гармоника почти зеркально симметрична относительно своего центра. Все эти явления особенно сильны на низких частотах, которые нам и важны при кодировании. Это плохо еще и тем, что на сжатом изображении будут заметны границы блоков. Проиллюстрирую DFT-базис с N=8. Первые 2 ряда - косинусные составляющие, последние - синусные:
Обратите внимание на появление дублей составляющих при повышении частоты. 
С первым дела крайне плохи.
Так может быть сделать как в DCT - уменьшить частоты в 2 или другое количество раз, чтобы количество некоторых колебаний было дробным и границы находились в разных фазах? Тогда составляющие будут неортогональны. И ничего тут не поделать.DST
Что если вместо косинусов в DCT использовать синусы? Мы получим Discrete Sine Transform (DST). Но для нашей задачи все они неинтересны, так как и целые и половинки периодов синусов близки к нулю на границах. То есть мы получим примерно такое же неподходящее разложение, как и у DFT.Возвращаясь к DCT
Как у него дела на границах? Хорошо. Есть противофазы и нет нулей.Все остальное
Не-Фурье преобразования. Не буду описывать.
WHT - матрица состоит только из ступенчатых составляющих со значениями -1 и 1.
Haar - по совместительству ортогональное вейвлет-преобразование.
Они уступают DCT, но легче для вычислений.
Будет непросто, правда? Впрочем, для некоторых типов изображений можно подобрать лучший базис, чем у DCT.Двумерные преобразования
Сейчас попробуем провести такой эксперимент. Возьмем, для примера, кусочек изображения.
Его 3D график:
Пройдемся DCT(N=32) по каждой строке:
Теперь я хочу, чтобы вы пробежались глазами по каждому столбцу полученных коэффициентов, т. е. сверху вниз. Вспомните, что наша цель - оставить как можно меньше значений, убрав малозначащие. Наверняка вы догадались, что значения каждого столбца полученных коэффициентов можно разложить точно так же, как и значения исходного изображения. Никто не ограничивает нас в выборе ортогональной матрицы преобразования, но мы сделаем это опять с помощью DCT(N=8):
Коэффициент (0,0) получился слишком большим, поэтому на графике он уменьшен в 4 раза.
Итак, что получилось?
Левый верхний угол - самые значащие коэффициенты разложения самых значащих коэффициентов.
Левый нижний угол - самые незначащие коэффициенты разложения самых значащих коэффициентов.
Правый верхний угол - самые значащие коэффициенты разложения самых незначащих коэффициентов.
Правый нижний угол - самые незначащие коэффициенты разложения самых незначащих коэффициентов.
Понятно, что значимость коэффициентов уменьшается, если двигаться по диагонали из левого верхнего угла в правый нижний. А какой важнее: (0, 7) или (7, 0)? Что они вообще означают?
Сначала по строкам: A 0 = (EX T) T = XE T (транспонировали, так как формула A=EX для столбцов), затем по столбцам: A=EA 0 = EXE T . Если аккуратно посчитать, то получится формула:
Таким образом, если вектор раскладывается на синусоиды, то матрица на функции вида cos(ax)*cos(by). Каждый блок 8x8 в JPEG представляется в виде суммы 64-х функций вида:
В Википедии и других источниках такие функции представлены в более удобной форме:
Поэтому коэффициенты (0, 7) или (7, 0) одинаково полезны.
Впрочем, фактически это обычное одномерное разложение на 64 64-мерных базиса. Все вышесказанное применимо не только к DCT, но и к любому ортогональному разложению. Действуя по аналогии, в общем случае получаем N-мерное ортогональное преобразование.
А вот уже 2-мерное преобразование енота (DCT 256x256). Опять же с обнуленными значениями. Числа - количество необнуленных коэффициентов из всех (оставлялись самые значимые значения, находящиеся в треугольной области в левом верхнем углу).
Запомните, что коэффициент (0, 0) называется DC, остальные 63 - AC. Выбор размера блока
Товарищ спрашивает : почему в JPEG используется разбиение именно 8x8. Из заплюсованного ответа:The DCT treats the block as if it were periodic and has to reconstruct the resulting jump at the boundaries. If you take 64x64 blocks, you"ll most likely have a huge jump at the boundaries, and you"ll need lots of high-frequency components to reconstruct that to a satisfactory precision
Мол, DCT работает хорошо только на периодических функциях, и если вы возьмете большой размер, то, скорее всего, получите гигантский скачок на границах блока и понадобится много высокочастотных компонентов для его покрытия. Это неверно! Такое объяснение очень похоже на DFT, но не на DCT, так как оно отлично покрывает такие скачки уже первыми составляющими.
На той же странице приводится ответ из MPEG FAQ, с основными аргументами против больших блоков:
Предлагаю самостоятельно исследовать это. Начнем с первого
.
По горизонтальной оси - доля первых необнуленных коэффициентов. По вертикальной - среднеквадратичное отклонение пикселей от оригинала. Максимальное возможное отклонение взято за единицу. Разумеется, для вердикта явно недостаточно одной картинки. К тому же, я действую не совсем правильно, просто обнуляя. В реальном JPEG, в зависимости от матрицы квантования, обнуляются только маленькие значения высокочастотных компонентов. Поэтому, следующие эксперименты и выводы предназначены для поверхностного выявления принципов и закономерностей.
Можно сравнить разбиение на разные блоки с оставленными 25-ю процентами коэффициентов (слева направо, затем справа налево):

Это значит, что, например, вычисление при разбиении на 64x64 в два раза сложнее, чем на 8x8.
Хотя искажения блоков 16x16 простираются дальше, чем у 8x8, но надпись более плавная. Поэтому меня убедили только первые два аргумента. Но мне что-то больше нравится разделение на 16x16.Квантование
На данном этапе мы имеем кучу матриц 8x8 с коэффициентами косинусного преобразования. Пришло время избавляться от малозначащих коэффициентов. Существует более элегантное решение, чем просто обнулять последние коэффициенты, как мы делали выше. Нас не устраивает этот способ, так как необнуленные значения хранятся с избыточной точностью, а среди тех, кому не повезло, могли оказаться достаточно важные. Выход - нужно использовать матрицу квантования. Потери происходят именно на это этапе. Каждый Фурье-коэффициент делится на соответствующее число в матрице квантования. Рассмотрим на примере. Возьмем первый блок от нашего енота и произведем квантование. В спецификации JPEG приводится стандартная матрица:
Стандартная матрица соответствует 50% качеству в FastStone и IrfanView. Такая таблица была выбрана с точки зрения баланса качества и степени сжатия. Думаю, что значение для DC-коэффициента больше соседних из-за того, что DCT ненормализовано и первое значение получается больше, чем следовало бы. Высокочастотные коэффициенты огрубляются сильнее из-за их меньшей важности. Думаю, сейчас такие матрицы используются редко, так как ухудшение качества хорошо заметно. Никто не запрещает использовать свою таблицу (со значениями от 1 до 255)
При декодировании происходит обратный процесс - квантованные коэффициенты почленно умножаются на значения матрицы квантования. Но так как мы округляли значения, то не сможем точно восстановить исходные коэффициенты Фурье. Чем больше число квантования, тем больше погрешность. Таким образом, восстановленный коэффициент является лишь ближайшим кратным.
Еще пример:

При восстановлении этого блока мы получим только усредненное значение плюс вертикальный градиент (из-за сохранившегося значения -1). Зато для него хранится всего два значения: 7 и -1. C другими блоками ситуация не лучше, вот восстановленная картинка:
А можете посмотреть матрицы квантования различных фотоаппаратов. Кодирование
Перед тем как двигаться дальше, нам нужно на более простых примерах понять, как можно сжать полученные значения.
Представьте такую ситуацию, что ваш знакомый забыл у вас дома листочек со списком и теперь просит продиктовать его по телефону (других способов связи нет).
Список:
Как бы вы облегчили свою задачу? Особого желания мучительно диктовать все эти слова у вас нет. Но их всего два и они повторяются. Поэтому вы просто как-нибудь диктуете первые два слова и договариваетесь, что далее «d9rg3» будете называть первым словом, а «wfr43gt» - вторым. Тогда достаточно будет продиктовать: 1, 2, 2, 1, 1, 1, 2, 1.
Закодировать ABC.
3-м разным символам (A, B, C) никак нельзя сопоставить 2 возможных значений бита (0 и 1). А раз так, то можно использовать по 2 бита на символ. Например:
Последовательность битов, сопоставленная символу, будем называть кодом. ABC будет кодироваться так: 000110. 
Закодировать AAAAAABC.
Использовать по 2 бита на символ A кажется немного расточительным. Что, если попробовать так:
Закодированная последовательность: 000000100.
Очевидно, этот вариант не подходит, так как непонятно, как декодировать первые два бита этой последовательности: как AA или как C? Использовать какой-нибудь разделитель между кодами очень расточительно, будем думать как по-другому обойти это препятствие. Итак, неудача произошла из-за того, что код C начинается с кода A. Но мы полны решимости кодировать A одним битом, пусть даже B и С будут по два. Исходя из такого пожелания, A дадим код 0. Тогда коды B и C не могут начинаться на 0. Но могут на 1:
Последовательность закодируется так: 0000001011. Попробуйте мысленно декодировать ее. Вы сможете сделать это только одним способом.
Мы выработали два требования к кодированию:
Очевидно, порядок символов не важен, нас интересует только частота их встречаемости. Поэтому, с каждым символом сопоставляют некоторое число, называемое весом. Вес символа может являться как относительной величиной, отражающий долю его вхождения, так и абсолютной, равной количеству символов. Главное, чтобы веса были пропорциональны встречаемости символов.
Рассмотрим общий случай для 4-х символов с любыми весами.
Без потери общности, положим pa ≥ pb ≥ pc ≥ pd. Существуют всего два принципиально разных по длинам кодов варианта:
Какое из них предпочтительнее? Для этого нужно вычислить получаемые длины закодированных сообщений:
W1 = 2*pa + 2*pb + 2*pc + 2*pd
W2 = pa + 2*pb + 3*pc + 3*pd
Если W1 меньше W2 (W1-W2<0), то лучше использовать первый вариант:
W1-W2 = pa - (pc+pd) < 0 => pa < pc+pd.
Если C и D вместе встречаются чаще других, то их общая вершина получает самый короткий код из одного бита. В противном случае, один бит достается символу A. Значит, объединение символов ведет себя как самостоятельный символ и имеет вес равный сумме входящих символов.
Вообще, если p - вес символа представленный долей его вхождения (от 0 до 1), то лучшая длина кода s=-log 2 p.
Рассмотрим это на простом случае (его легко представить в виде дерева). Итак, нужно закодировать 2 s символов с равными весами (1/2 s). Из-за равенства весов длины кодов будут одинаковыми. Каждому символу потребуется s бит. Значит, если вес символа 1/2 s , то его длина s. Если вес заменить заменить на p, то получим длину кода s=-log 2 p . Значит, если один символ встречается в два раза реже другого, то длина его кода будет на бит длиннее. Впрочем такой вывод легко сделать, если вспомнить, что добавление одного бита позволяет в два раза увеличить количество возможных вариантов.
И еще одно наблюдение - два символа с наименьшими весами всегда имеют наибольшие, но равные длины кодов. Более того, их биты, кроме последнего, совпадают. Если бы это было неверно, то, по крайней мере, один код можно было бы укоротить на 1 бит, не нарушая префиксности. Значит, два символа с наименьшими весами в кодовом дереве имеют общего родителя уровнем выше. Вы можете видеть это на примере С и D выше.
Попробуем решить следующий пример, по выводам, полученным в предыдущем примере.
Шаги повторяются, пока не останется только одна группа. В каждой группе одному символу (или подгруппе) присваивается бит 0, а другому бит 1.
Этот алгоритм называется кодированием Хаффмана.
На иллюстрации приведен пример с 5-ю символами (A: 8, B: 6, C: 5, D: 4, E: 3). Справа указан вес символа (или группы).
Кодируем коэффициенты
Возвращаемся. Сейчас мы имеем много блоков с 64-я коэффициентами в каждом, которые нужно как-то сохранить. Самое простое решение - использовать фиксированное количество бит на коэффициент - очевидно, неудачное. Построим гистограмму всех полученных значений (т.е. зависимость количества коэффициентов от их значения):
Обратите внимание - шкала логарифмическая! Сможете объяснить причину появления скопления значений превышающих 200? Это DC-коэффициенты. Так как они сильно отличаются от остальных, то неудивительно, что их кодируют отдельно. Вот только DC:
Обратите внимание, что форма графика напоминает форму графиков из самих ранних экспериментов деления на пары и тройки пикселей
Вообще, значения DC-коэффициентов могут меняться от 0 до 2047 (точнее от -1024 до 1023, так как в JPEG производится вычитание 128 из всех исходных значений, что соответствует вычитанию 1024 из DC) и распределяться довольно равномерно с небольшими пиками. Поэтому кодирование Хаффмана здесь не очень-то поможет. А еще представьте, каким большим будет дерево кодирования! И во время декодирования придется искать в нем значения. Это очень затратно. Думаем дальше.
DC-коэффициент - усредненное значение блока 8x8. Представим градиентный переход (пусть не идеальный), который часто встречается в фотографиях. Сами DC значения будут разными, но они будут представлять арифметическую прогрессию. Значит, их разность будет более-менее постоянна. Построим гистограмму разностей:
Вот это уже лучше, потому что значения, в целом, сконцентрированы около нуля (но алгоритм Хаффмана опять даст слишком большое дерево). Маленькие значения (по абсолютной величине) встречаются часто, большие редко. А так как маленькие значения занимают мало бит (если убрать ведущие нули), то хорошо выполняется одно из правил сжатия: символам с большими весами присваивать короткие коды (и наоборот). Нас пока ограничивает невыполнение другого правила: невозможность однозначного декодирования. В целом, такая проблема решается следующими способами: заморочиться с кодом-разделителем, указывать длину кода, использовать префиксные коды (они вам уже известны - это случай, когда ни один код не начинается с другого). Пойдем по простому второму варианту, т. е. каждый коэффициент (точнее, разница соседних) будет записываться так: (длина)(значение), по такой табличке:
То есть положительные значения прямо кодируются их двоичным представлением, а отрицательные - так же, но с заменой ведущей 1 на 0. Осталось решить, как кодировать длины. Так как их 12 возможных значений, то можно использовать 4 бита для хранения длины. Но вот тут-то как раз лучше использовать кодирование Хаффмана.
Значений с длинами 4 и 6 больше всего, поэтому им достались самые короткие коды (00 и 01).
Может возникнуть вопрос: почему на примере у значения 9 код 1111110, а не 1111111? Ведь можно смело поднять «9» на уровень выше, рядом с «0»? Дело в том, что в JPEG нельзя использовать код, состоящий только из единиц - такой код зарезервирован.
Есть еще одна особенность. Коды, полученные описанным алгоритмом Хаффмана могут не совпасть по битам с кодами в JPEG, хотя их длины будут одинаковыми. Используя алгоритм Хаффмана, получают длины кодов, а сами коды генерируются (алгоритм прост - начинают с коротких кодов и добавляют их по очереди в дерево как можно левее, сохраняя свойство префиксности). Например, для дерева выше хранится список: 0,2,3,1,1,1,1,1. И, разумеется, хранится список значений: 4,6,3,5,7,2,8,1,0,9. При декодировании коды генерируются таким же способом.
[код Хаффмана для длины DC diff (в битах)]
где DC diff = DC текущее - DC предыдущее 
Так как график очень похож на график для разностей DC, то принцип тот же: [код Хаффмана для длины AC (в битах)]. Но не совсем! Так как на графике шкала логарифмическая, то не сразу заметно, что нулевых значений примерно в 10 раз больше, чем значения 2 - следующего по частоте. Это понятно - не все пережили квантование. Вернемся к матрице значений, полученной на этапе квантования (используя матрицу квантования FastStone, 90%).
Так как встречается много групп подряд идущих нулей, то появляется идея - записывать только количество нулей в группе. Такой алгоритм сжатия называется RLE (Run-length encoding, кодирование повторами). Осталось выяснить направление обхода «подряд идущих» - кто за кем? Выписать слева направо и сверху вниз - не очень эффективно, так как ненулевые коэффициенты концентрируются около левого верхнего угла, а чем ближе к правому нижнему - тем больше нулей.
Поэтому, в JPEG используется порядок, называемый «Zig-zag», он показан на левом рисунке. Такой способ хорошо выделяет группы нулей. На правом рисунке - альтернативный способ обхода, не относящийся к JPEG, зато с любопытным названием (пруф). Он может использоваться в MPEG при сжатии видео с чересстрочной разверткой. Выбор алгоритма обхода не влияет на качество изображения, но может увеличить количество кодируемых групп нулей, что в итоге может отразиться на размере файла.
Модифицируем нашу запись. Для каждого ненулевого AC - коэффициента:
[Количество нулей перед AC][код Хаффмана для длины AC (в битах)]
Думаю, что вы сразу скажете - количество нулей тоже отлично закодируется Хаффманом! Это очень близкий и неплохой ответ. Но можно немного оптимизировать. Представьте, что имеем некоторый коэффициент AC, перед которым было 7 нулей (разумеется, если выписывать в зигзагообразном порядке). Эти нули - дух значений, которые не выдержали квантования. Скорее всего, наш коэффициент тоже сильно потрепало и он стал маленьким, а, значит, его длина - короткой. Значит, количество нулей перед AC и длина AC - зависимые величины. Поэтому записывают так:
[код Хаффмана для (Количество нулей перед AC, длина AC (в битах)]
Алгоритм кодирования остается тем же: те пары (количество нулей перед AC, длина AC), которые встречаются часто, получат короткие коды и наоборот.
Длинный «горный хребет» подтверждает наше предположение.
Такая пара занимает 1 байт: 4 бита на количество нулей и 4 бита на длину AC. 4 бита - это значения от 0 до 15. Для длины AC хватит с избытком, но ведь нулей может быть больше 15? Тогда используется больше пар. Например, для 20 нулей: (15, 0)(5, AC). То есть, 16-й ноль кодируется как ненулевой коэффициент. Так как ближе к концу блока всегда полно нулей, то после последнего ненулевого коэффициента используется пара (0,0). Если она встретится при декодировании, значит оставшиеся значения равны 0.
[код Хаффмана для длины DC diff ]
[код Хаффмана для (количество нулей перед AC 1 , длина AC 1 ]
…
[код Хаффмана для (количество нулей перед AC n , длина AC n ]
Где AC i - ненулевые AC коэффициенты.Цветное изображение
Способ представления цветного изображения зависит от выбранной цветовой модели. Простое решение - использовать RGB и кодировать каждый цветовой канал изображения по отдельности. Тогда кодирование не будет отличаться от кодирования серого изображения, только работы в 3 раза больше. Но сжатие изображения можно увеличить, если вспомнить, что глаз более чувствительнее к изменению яркости, чем цвета. Это значит, что цвет можно хранить с бОльшими потерями, чем яркость. У RGB нет отдельного канала яркости. Она зависит от суммы значений каждого канала. Поэтому, RGB-куб (это представление всех возможных значений) просто «ставят» на диагональ - чем выше, тем ярче. Но на этом не ограничиваются - куб немного поджимают с боков, и получается скорее параллелепипед, но это лишь для учета особенностей глаза. Например, он более восприимчив к зеленому, чем синему. Так появилась модель YCbCr.
(Изображение с Intel.com)
Y - компонента яркости, Cb и Cr являются синей и красной цветоразностными компонентами. Поэтому, если хотят сильнее сжать изображение, то RGB переводят в YCbCr, и каналы Cb и Cr прореживают. То есть разбивают на небольшие блоки, например 2x2, 4x2, 1x2, и усредняют все значения одного блока. Или, другими словами, уменьшают размер изображения для этого канала в 2 или 4 раза по вертикали и/или горизонтали. 
Каждый блок 8x8 кодируется (DCT + Хаффман), и закодированные последовательности записываются в таком порядке:
Любопытно, что спецификация JPEG не ограничивает в выборе модели, то есть реализация кодировщика может как угодно разделить изображение по цветовым компонентам (каналам) и каждый будет сохранен по отдельности. Мне известно об использовании Grayscale (1 канал), YCbCr (3), RGB (3), YCbCrK (4), CMYK (4). Первые три поддерживаются почти всеми, а вот с последними 4-канальными бывают проблемы. FastStone, GIMP поддерживают их корректно, а штатные программы Windows, paint.net корректно извлекают всю информацию, но потом выбрасывают 4 черный канал, поэтому (Antelle сказал, что не выбрасывают, читайте его комментарии) показывают более светлое изображение. Слева - классический YCbCr JPEG, справа CMYK JPEG:

Если они различаются по цветам, или видна только одна картинка, то, скорее всего, у вас IE (любой версии) (UPD. в комментариях говорят «или Safari»). Можете попробовать открыть статью в разных браузерах.И еще кое-что
В двух словах о дополнительных возможностях.Progressive mode
Разложим полученные таблицы коэффициентов DCT на сумму таблиц (примерно так (DC, -19, -22, 2, 1) = (DC, 0, 0, 0, 0) + (0, -20, -20, 0, 0) + (0, 1, -2, 2, 1)). Сначала закодируем все первые слагаемые (как мы уже научились: Хаффман и обход зигзагом), затем вторые и т. д. Такой трюк полезен при медленном интернете, так как сперва загружаются только DC коэффициенты, по которым строится грубая картинка c «пикселями» 8x8. Затем округленные AC коэффициенты, позволяющие уточнить рисунок. Затем грубые поправки к ним, затем более точные. Ну и так далее. Коэффициенты округляются, так как на ранних этапах загрузки точность не столь важна, зато округление положительно сказывается на длине кодов, так как для каждого этапа используется своя таблица Хаффмана.Lossless mode
Сжатие без потерь. DCT нет. Используется предсказание 4-й точки по трем соседним. Ошибки предсказания кодируются Хаффманом. По-моему, используется чуть чаще, чем никогда.Hierarhical mode
По изображению создается несколько слоев с разными разрешениями. Первый грубый слой кодируется как обычно, а затем только разница (уточнение изображения) между слоями (прикидывается вейвлетом Хаара). Для кодирования используется DCT или Lossless. По-моему, используется чуть реже, чем никогда.Арифметическое кодирование
Алгоритм Хаффмана создает оптимальные коды по весу символов, но это верно только для фиксированного соответствия символов с кодами. Арифметическое не имеет такой жесткой привязки, что позволяет использовать коды как бы с дробным числом бит. Утверждается, что оно уменьшает размер файла в среднем на 10% по сравнению с Хаффманом. Не распространено из-за проблем с патентом, поддерживается не всеми.
vanwin предложил указать использованное ПО. С удовольствием сообщаю, что все доступны и бесплатны:




 .
.




